Дан параллелепипед ABCDA1B1C1D1, разложите векторы: а) вектор DB1 по трём некомпланарным векторам б) вектор AC1 по векторам: AO, AN, AK, где точки O, N, K - середины AB, AD, AA1 в) вектор BD по векторам: A1A, A1B, A1D1
Приведу редко используемый в этой ситуации в надежде. что кто-нибудь другой даст и один из стандартных .
Пусть K - точка касания одной из двух касательных с окружностью. Тогда KN=\sqrt{10} - ведь уравнение окружности x²+(y-1)^2=10, центр у нее в точке N(0;1), а радиус равен корню из 10.
Далее, поскольку касательная перпендикулярна радиусу, проведенному в точку касания, угол MKN прямой, KM²=50-10=40, а тангенс угла KMN равен
Поэтому. чтобы получить касательную, нужно прямую MN с угловым коэффициентом (то есть тангенсом угла наклона) 1/7 повернуть вокруг точки M на угол arctg(1/2) в ту или другую сторону. Поскольку
сначала строим график данной функции: 1) Чертим систему координат, отмечаем точку О - начало отсчёта, отмечаем стрелками положительное направление вправо и вверх; подписываем названия осей: вправо - ось х, вверх - ось у отмечаем единичные отрезки по каждой оси в 1 клетку 2) график у= 2х-3 - прямая, для построения нужны две точки, занесём их координаты в таблицу: х= 0 2 у= -3 1 Поставим точки (0; -3) и (2; 1) в системе координат; проведём через них прямую линию; подпишем график функции у = 2х - 3 График построен!
Переходим ко второму заданию: находим на оси ординат у = -1, смотрим какая точка по оси х соответствует графику, видим х = 1
находим на оси абсцисс, х = 3, смотрим какая точка по оси у соответствует графику, видим у = 3
Приведу редко используемый в этой ситуации в надежде. что кто-нибудь другой даст и один из стандартных .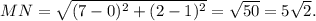
Пусть K - точка касания одной из двух касательных с окружностью. Тогда KN=\sqrt{10} - ведь уравнение окружности x²+(y-1)^2=10, центр у нее в точке N(0;1), а радиус равен корню из 10.
Далее, поскольку касательная перпендикулярна радиусу, проведенному в точку касания, угол MKN прямой, KM²=50-10=40, а тангенс угла KMN равен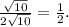
Поэтому. чтобы получить касательную, нужно прямую MN с угловым коэффициентом (то есть тангенсом угла наклона) 1/7 повернуть вокруг точки M на угол arctg(1/2) в ту или другую сторону. Поскольку
Поэтому уравнения касательных -
сначала строим график данной функции:
1) Чертим систему координат, отмечаем точку О - начало отсчёта, отмечаем стрелками положительное направление вправо и вверх;
подписываем названия осей: вправо - ось х, вверх - ось у
отмечаем единичные отрезки по каждой оси в 1 клетку
2) график у= 2х-3 - прямая, для построения нужны две точки, занесём их координаты в таблицу:
х= 0 2
у= -3 1
Поставим точки (0; -3) и (2; 1) в системе координат; проведём через них прямую линию; подпишем график функции у = 2х - 3
График построен!
Переходим ко второму заданию:
находим на оси ординат у = -1, смотрим какая точка по оси х соответствует графику, видим х = 1
находим на оси абсцисс, х = 3, смотрим какая точка по оси у соответствует графику, видим у = 3