Дана функция y=f(x) с указанной областью определения. Запишите обратную к ней функцию указав в виде у =h(x), ее область определения постройте на одном чертеже график функции f и g 1) f(x) =2x -3; D: R; 2) f(x) = 2x + 1, D: x (больше или равно) 0
3) f (x) = 1/x-2 D: x(меньше или равно) 3
4)f(x) = x^2 D: (-(бесконечность) ; 0]
5) f(x) = √x-1, D [1; + (Бесконечность)

Пошаговое объяснение:

чтобы найти обратную функцию надо из уравнения функции выразить x через y, потом переобозначить x и y, вот и получится обратная функция к данной.

1) y =2x -3; D: R;

D: x∈R;

2)  y = 2x + 1, D: x ≥ 0

обратная

3)  y = 1/x-2 D: x≤3

запись не понятна, делаю оба варианта

а) (1/x)-2    D: x≤3

обратная

1/(х+2)  D: x≤3 по поводу х≠-2 волноваться не стоит, т.к 1/(х+2) вообще существует на интервале (-2; +∞)

б) 1/(х-2)   D: x≤3

обратная

здесь обе гиперболы не пересекают ось Х (т.е.х≠0 по определению)

4)y = x² D: х∈(-∞ ; 0]

обратная

y=±√x; D: x∈[0; +∞)

5)  y = √x-1, D x∈[1; + ∞)

a) y = √(x)-1, D x∈[1; + ∞)

D x∈[1; + ∞)

обратная

  D: x∈[1; + ∞)

б)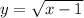   D: x∈[1; + ∞)

обратная

х² +1 ;  D: x∈[1; + ∞)

файлы графиков плоховато видны, просто потупайте мышью в места, где должны быть файлы - они откроются

для последней функции файлы графиков не присоединяются.

ну, надеюсь, Вы их построите самостоятельно.