Задачу можно решить подбором. Предположим, самое маленькое количество выполненных задач - 1, а самое большое - 6. Тогда плучается, что белки решили 4 задачи. 4 можно разложить лишь на 2 и 2 или 3 и 1. Ни то, ни другое не подходит.
Предположим, самое маленькое - 1, самое большое - 5. Тогда получается, что белки решили 5 задач. 5 можно разложить на 3 и 2. Это решение вполне подходит.
(Перебирая 4, 3 и 2, вы поймете, почему я не стала их брать в пример. Просто они слишком маленькие, чтобы быть самыми большими)
Пусть х- масса коктейля
Приймемо весь коктейль за одиницю, тогда
х - 1
350 - 0.7
составим пропорцию
х/350=1/0.7
х=350*1/0.7= 500 (г) - масса коктейля.
Тогда масса сиропа:
500*3/20= 75 (г)
Масса ванилина:
500*1/10= 50 (г)
Масса какао:
500*1/20=25и (г)
Примем все нити за 1, тогда белых нитей было
1-1/10-2/5-3/20=20/20-2/20-8/20-3/20=(20-2-8-3)/20=7/20
Пусть всех нитей - х (г), тогда
х - 1
700 - 7/20
составим пропорцию
х/700=1/720
х=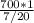
=2000 (г)
Тогда масса ниток красного цвета:
2000*1/10=200
-синего:
2000*2/5 =800
коричневого:
2000*3/20= 300
Задачу можно решить подбором. Предположим, самое маленькое количество выполненных задач - 1, а самое большое - 6. Тогда плучается, что белки решили 4 задачи. 4 можно разложить лишь на 2 и 2 или 3 и 1. Ни то, ни другое не подходит.
Предположим, самое маленькое - 1, самое большое - 5. Тогда получается, что белки решили 5 задач. 5 можно разложить на 3 и 2. Это решение вполне подходит.
(Перебирая 4, 3 и 2, вы поймете, почему я не стала их брать в пример. Просто они слишком маленькие, чтобы быть самыми большими)
Значит, победили ежи! Ура, товарищи!