Юля начала смотреть фильм в 15:00.
Но тут сказано, что если бы она начала смотреть на 15 минут раньше, то он закончился бы в 16:15.
То есть, начало фильма 15:00 - 15 минут = 14:45, конец в 16:15.
Значит фильм идет - 1 час 30 минут.
Юля начала смотреть фильм и одновременно поставила мясо в духовку.
А когда мясо приготовилось, она ела его оставшиеся 45 минут.
Теперь нужно вычесть из времени фильма время ужина.
1 час 30 минут - 45 минут = 45 минут - готовилось мясо.
Переводим в секунды: 45 минут = 45 * 60 = 2 700 секунд.
ответ: 2 700 сек.
Правильная четырехугольная пирамида .
(см²).
(см).
- сторону основания.
Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
, где - сторона основания и - апофема (высота боковой грани, проведенная из вершины).
Попробуем выразить через (сторону основания) и (см) (высоту пирамиды).
Рассмотрим прямоугольный (где - середина ). В нем (см), а (см) (как половина стороны квадрата, равной см).
По теореме Пифагора:
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что - неотрицательное):
Пусть :
Второй корень нам не подходит по причине отрицательности. Значит:
Задача решена!
Юля начала смотреть фильм в 15:00.
Но тут сказано, что если бы она начала смотреть на 15 минут раньше, то он закончился бы в 16:15.
То есть, начало фильма 15:00 - 15 минут = 14:45, конец в 16:15.
Значит фильм идет - 1 час 30 минут.
Юля начала смотреть фильм и одновременно поставила мясо в духовку.
А когда мясо приготовилось, она ела его оставшиеся 45 минут.
Теперь нужно вычесть из времени фильма время ужина.
1 час 30 минут - 45 минут = 45 минут - готовилось мясо.
Переводим в секунды: 45 минут = 45 * 60 = 2 700 секунд.
ответ: 2 700 сек.
Правильная четырехугольная пирамида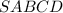 .
.
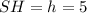 (см).
(см).
Найти: - сторону основания.
- сторону основания.
Решение:Площадь боковой поверхности правильной четырехугольной пирамиды можно вычислить по следующей формуле:
Попробуем выразить через
через  (сторону основания) и
(сторону основания) и 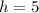 (см) (высоту пирамиды).
(см) (высоту пирамиды).
Рассмотрим прямоугольный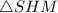 (где
(где 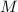 - середина
- середина 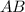 ). В нем
). В нем 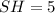 (см), а
(см), а 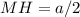 (см) (как половина стороны квадрата, равной
(см) (как половина стороны квадрата, равной  см).
см).
По теореме Пифагора:
Все это подставляем в уравнение площади боковой поверхности (при возведении в квадрат держим в голове, что - неотрицательное):
- неотрицательное):
Пусть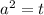 :
:
Второй корень нам не подходит по причине отрицательности. Значит:
Задача решена!
ответ: