Пусть - сторона куба В, тогда
- площадь грани куба В.
пусть - сторона куба А, тогда
- площадь грани куба А.
По условию
на 69%
Если принять за 100%, тогда
100% + 69% = 169% - это
Получаем соотношение между площадями куба А и куба В:
Решаем:
Так как , то
это соотношение между сторонами куба А и куба В.
- объем куба В
объем куба А
Если объем куба В составляет 100%, то
объем куба А составит: 2,197 · 100% = 219,7%
Наконец, находим на сколько процентов объем куба А больше объема куба В:
219,7% - 100% = 119,7%
ответ: на 119,7%
Пусть - сторона куба В, тогда
- сторона куба В, тогда
пусть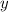 - сторона куба А, тогда
- сторона куба А, тогда
По условию
Если принять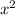 за 100%, тогда
за 100%, тогда
100% + 69% = 169% - это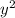
Получаем соотношение между площадями куба А и куба В:
Решаем:
Так как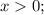
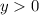 , то
, то
Если объем куба В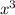 составляет 100%, то
составляет 100%, то
объем куба А составит: 2,197 · 100% = 219,7%
Наконец, находим на сколько процентов объем куба А больше объема куба В:
219,7% - 100% = 119,7%
ответ: на 119,7%