Даны координаты вершин пирамиды a(-9; -7; 4), b(-4; 3; -1), c(5; -4; 2) и d(3; 4; 4). найти: a)объем пирамиды б)площадь сечения, проходящего через середину ребра cd и вершины a и b в)косинус угла между ребрами ca и cb.
Х-скорость красного у- скорость синего АВ-ширина реки Т.к. скорости равномерны, отношение этих скоростей будет равно отношению пройденных расстояний См. рисунок х:у=900:(АВ-900) х:у=(АВ-900+300):(900+АВ-300)=(АВ-600):(АВ+600)
Пошаговое объяснение:
1.
Перенесем 42 вправо, поменяв знак на противоположный, приведем подобные члены и найдем х, разделив обе части уравнения на числовой коэффициент при х:
Чтобы найти делимое, надо частное умножить на делитель:
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность:
2.
1-я сторона - ? в три раза больше 2-й;
2-я сторона - ? на 8 меньше 3-й;
3-я сторона - ?
Периметр Р=98
Пусть вторая сторона - х, тогда первая сторона - 3х, а третья - (х+8)
Периметр - сумма длин всех сторон.
Составим уравнение:
⇒ 2-я сторона - 18; 1-я сторона - 54; 3-я сторона - 26.
3.
Распределительное свойство: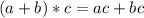
4.
Приведем подобные члены:
у- скорость синего
АВ-ширина реки
Т.к. скорости равномерны, отношение этих скоростей будет равно отношению пройденных расстояний
См. рисунок
х:у=900:(АВ-900)
х:у=(АВ-900+300):(900+АВ-300)=(АВ-600):(АВ+600)
900:(АВ-900)=(АВ-600):(АВ+600) или
900 (АВ-600)
------------ = -------------
(АВ-900) (АВ+600)
900(АВ+600)=(АВ-900)(АВ-600)
900АВ+540000=АВ^2-600АВ-900АВ+540000
АВ^2-600АВ-900АВ+540000-900АВ-540000=0
АВ^2-2400АВ=0
АВ(АВ-2400)=0
АВ₁=0 - не подходит
АВ₂-2400=0
АВ₂=2400м=2км400м=2,4км -ширина реки