Пусть X и Y - два данных шестизначных числа, тогда:
X*1000000+Y=X*Y*n, где n ∈ N
X*(Y*n - 1000000) = Y - отсюда Y = X*k, где k ∈ N, k<9. Далее подставляем: Y=X*k ⇒ X*n*k - 1000000 = k. Числа переносим в одну сторону, коэффициенты в другую, вынеся при этом общий множитель k:
k*(X*n - 1) = 1000000
k равно 2 или 5 ⇒ X*n равно 500001 или 200001, однако если n=1, тогда Y будет семизначным, если k>1 и делит 200001, тогда Y будет пятизначным. Соответственно: a*k равно только 500001 и n=3. Отсюда:
возможны три случая:
1)в числе две единицы и две двойки
таких чисел: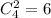
, т.к. мы выбираем две любые позиции для единиц и в остальных двух будут двойки
2) в числе две единицы и одна двойка
таких чисел: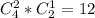
, снова выбираем две позиции для единицы и одну позицию из двух оставшихся для двойки
3) в числе две двойки и одна единица
аналогично предыдущему 12 таких чисел
больше случаев быть не может, т.к. в числе обязательно либо две единицы, либо две двойки, т.к. всего 5 цифр дано
всего чисел: 6 + 12 + 12 = 30
ответ: 30 чисел
Пусть X и Y - два данных шестизначных числа, тогда:
X*1000000+Y=X*Y*n, где n ∈ N
X*(Y*n - 1000000) = Y - отсюда Y = X*k, где k ∈ N, k<9. Далее подставляем: Y=X*k ⇒ X*n*k - 1000000 = k. Числа переносим в одну сторону, коэффициенты в другую, вынеся при этом общий множитель k:
k*(X*n - 1) = 1000000
k равно 2 или 5 ⇒ X*n равно 500001 или 200001, однако если n=1, тогда Y будет семизначным, если k>1 и делит 200001, тогда Y будет пятизначным. Соответственно: a*k равно только 500001 и n=3. Отсюда:
X = 166667, Y = 333334
⇒ ответ: 166667333334=3*166667*333334