Даны соответствия между элементами двух множеств. Закрасьте фигуру с ответом «да», если данные соответствия являются функциями, и фигуру с ответом «нет» в противном случае.

Особенности арабо-мусульманской философии.Особенности арабо-мусульманской философии определялись в Средние века исключительными условиями ее развития. На арабском Востоке и в части Испании, покоренной арабами, философская мысль находилась под гораздо меньшим воздействием религии, чем в Европе и Восточной Азии. Кроме того, объединение разрозненных арабских племен в единое огромное государство (Халифат средоточию лучших умов в его научных центрах и достижению наиболее высокого уровня развития философской мысли. Ее формировали представители многочисленных народов, населяющих это государство: арабы, персы, евреи, таджики, турки, узбеки и т.д. Но все учения излагались только на арабском языке. Поэтому философию многих восточных народов принято называть арабоязычной. Еще одна ее особенность состоит в том, что она развивалась не только на фоне мифологий разных восточных народов, молодой тогда и посему не очень влиятельной религии - исламе, но и на базе высокоразвитой науки. В этой связи необходимо подчеркнуть, что арабская и арабоязычная наука в этот период ушла далеко вперед по сравнению с европейской.В VIII—IX веках культурное развитие Западной Европы находилось еще на крайне, низком уровне по сравнению с арабским Востоком, где уже расцветала мощная и самобытная культура. Если обратиться к отдельным наукам, развитию которых арабы, то на одно из первых мест надо поставить географию. Географический кругозор арабов намного превосходил античный. Это естественно, если иметь в виду обширные районы, завоеванные ими. В тесной связи с географией находилась астрономия. Основной труд древности, творение Птолемея, сохранился благодаря арабам и известен под названием «Альмагесты». Аль-Зуфи в X веке впервые изготовил звездный каталог, где не только представлено положение звезд, но и указана их величина. Безусловны заслуги арабов в математике. Именно они ввели арабские цифры в арифметику, сделали переводы трудов Евклида по геометрии. Арабы значительно упростили тригонометрические вычисления греков. Велики заслуги арабов в физике и химии. Они ввели в европейский обиход ряд важных технических новинок: водяные и механические часы, хлопчатую, а затем и льняную бумагу, порох и многое другое.В медицине арабы также добились значительных успехов. Наблюдения и описания болезней, сделанные арабскими врачами, отличаются большой точностью. Именно рабы впервые описали признаки таких распространенных болезней, как корь, оспа, рахит. Они значительно обогатили фармакологию. Многие арабские медики славились и как философы, например, Ибн-Сина (Авиценна). Расцвет арабской культуры (науки, искусства, техники, медицины) на рубеже I—II тысячелетий отразился на содержании философии. Внимание к опытному знанию и естественнонаучным дисциплинам принципиально отличает арабских философов Средневековья от их коллег европейцев. Однако в начальной форме арабской философской мысли, которую называли «калам», доминировали логические рассуждения о религиозных догмах Корана. Калам можно назвать магометанской схоластикой, так как он тоже обслуживал религию, «теоретически» оправдывая богословие.Возник калам в начале VIII века. Один из авторов прямо называет его метафизическим учением о сущности Бога, его атрибутах. Попытка поддержать ортодоксальную веру путем прибавления к ней «небольшой дозы» рациональных элементов была предпринята в X веке Аль-Ашари (873-935). Однако некоторые предлагаемые им рациональные элементы доказательства бытия Бога были столь мизерны, что они почти не затрагивали веру в магию или в чудеса святых и т.п. Свободная Божья воля творит чудеса, воздействуя абсолютно на все явления природы. Так, тень есть не результат отсутствия освещения, а следствие Божьей воли. То есть нет никакой необходимой связи между причиной и следствием. Гегель в связи с этим остроумно назвал такой подход «шатанием, головокружением всего существующего» [14].Постепенно у арабов развилась собственная оригинальная философия, в определенной мере связанная с теологией

ОДЗ:

2-х≥0⇒  х≤2

Возводим в квадрат при условии, что a-x ≥0, т. е x ≤a

2-х=(а-х)²

2-х=а²-2ах+х²

х²-(2а-1)х+а²-2=0

D=(2a-1)²-4(a²-2)=4a²-4a+1-4a²+8=9-4a

Если D=0 ⇒  квадратное уравнение имеет один корень

9-4а=0

а=2,25     уравнение x²-3,5x+(49/16)=0⇒(x-1,75)²=0

x=1,75  - входит в ОДЗ.

x=1,75  -    корень уравнения

Если D>0 ⇒  квадратное уравнение имеет два  корня

D>0;  D=9-4a ⇒9-4a >0  ⇒  a < 2,25

C учетом ОДЗ: x≤2   и условия: x≤a

при  2 ≤а<2,25  уравнение имеет два корня.

Значит, при a ∈(-∞;-2) U {2,25}  уравнение имеет один корень

О т в е т.  a ∈(-∞;-2) U {2,25}

Графический решения.

√(2-x)=a-x

√(2-x)+x=a

Уравнение имеет вид: f(x)=g(x)

f(x)=√(2-x)+x;  g(x)=а

Строим график функции y=√(2-x)+x

Область определения x ∈(-∞;2]

y`=0

   ⇒             ⇒    -  точка возможного экстремума функции.

Применяем достаточное условие экстремума:

проверяем знак производной при переходе через точку.

При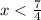          y` >0   функция возрастает

При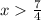         y` < 0   функция убывает

y_(наиб) = y (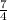 ) = = 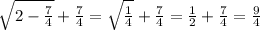2,25

Прямая y=a  пересекает график функции в одной точке

при a ∈ (-∞;2)  и  при a=2,25

О т в е т. a ∈ (-∞;2)  U{2,25}