Даны вершины А1(7; 0; 3), A2(3; 0; -1), A3(3; 0; 5), A4(4; 3; -2). Средствами векторной алгебры найти: а) длину ребра А1A2; б) угол между ребрами А1A2 и А1A3; в) площадь грани А1A2A3; г) длину высоты пирамиды, проведенной из вершины A4; д) объем пирамиды А1A2A3A4.

1. Длина окружности может быть определена по формуле:

C = π*d = 3,14*35 = 109,9 см

где d – диаметр.

2. Масштаб 1:1000 подразумевает, что на карте все линейные размеры уменьшены в 1000 раз по сравнению с реальными. Отсюда:

L = 9,6*1000 = 9600 см или 96 м

3. Площадь круга может быть определена по формуле

S = π*r^2 = π*7^2 = 3,1*49 = 151.9 дм^2

где r – радиус.

4. Процент снижения цены товара определится:

p =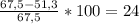

5. Площадь прямоугольника определяется по формуле:

S = a*b

где a, b – стороны.

Каждая сторона в 500 раз больше, чем на плане (см. задачу 2), таким образом, реальная площадь прямоугольного участка:

Sр = 500*a*500*b = 250000*S = 250000*25 = 6250000 см^2 или 625 м^2

1. Длина окружности может быть определена по формуле:

C = π*d = 3,14*35 = 109,9 см

где d – диаметр.

2. Масштаб 1:1000 подразумевает, что на карте все линейные размеры уменьшены в 1000 раз по сравнению с реальными. Отсюда:

L = 9,6*1000 = 9600 см или 96 м

3. Площадь круга может быть определена по формуле

S = π*r^2 = π*7^2 = 3,1*49 = 151.9 дм^2

где r – радиус.

4. Процент снижения цены товара определится:

p =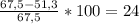

5. Площадь прямоугольника определяется по формуле:

S = a*b

где a, b – стороны.

Каждая сторона в 500 раз больше, чем на плане (см. задачу 2), таким образом, реальная площадь прямоугольного участка:

Sр = 500*a*500*b = 250000*S = 250000*25 = 6250000 см^2 или 625 м^2