Десять шахматистов за девять дней сыграли полный однокруговой турнир, в ходе которого каждый из них сыграл с каждым ровно одну партию. Каждый день игралось ровно пять партий, каждый шахматист был задействованы ровно в одной из них. Для какого максимального n 9 можно утверждать, что, независимо от расписания, в конце некоторого игрового дня с номером k 8 обязательно найдутся n шахматистов, уже сыгравших между собой все положенные в турнире партии?
Пошаговое объяснение:
3) Площадь круга: S=πR²
Измеряешь горизонтальную сторону прямоугольника и делишь ее на 2. Это значение -радиус(R).
Считаешь S= 3*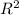 . Так мы нашли S круга.
. Так мы нашли S круга.
Дальше находим площадь прямоугольника: S=ab
Умножаешь длину на ширину, узнаешь площадь прямоугольника.
Теперь из площади прямоугольника вычитаешь площадь круга, то есть
Площадь закрашенной фигуры равна:
S= ab - 3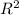
4) Фигура состоит из 2 фигур(см.картинку):
Из прямоугольника со сторонами 8 и 7.(Его площадь равна S=ab=56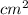 )
)
и прямоугольника со сторонами 4 и 5. (Его площадь равна S=ab=20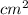 )
)
Площадь фигуры =76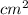 =7600
=7600 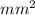
ответ:Пусть х – количество яблок на каждой из веток после сбора.
Тогда первоначально на первой ветке было (х + 3) яблок.
На второй ветке первоначально было (х + х/2) = 1,5х яблок.
А на третьей ветке было (х + 2х) = 3х яблок.
Составим уравнение:
(х + 3) + 1,5х + 3х = 80,
5,5х = 77,
х = 14.
То есть сейчас на каждой из веток по 14 яблок.
Значит первоначально на ветках было:
- на первой ветке (х + 3) = (14 + 3) = 17 яблок,
- на второй ветке 1,5х = 1,5 * 14 = 21 яблоко,
- на третьей ветке 3х = 3 * 14 = 42 яблока.
ответ: на первой ветке первоначально было 17 яблок, на второй ветке было 21 яблоко, а на третьей – 42 яблока.