10. У нас дано, что A⊂B.
Докажем, что (C\B)⊂(C\A).
Доказательство.
Пусть x∈C\B, тогда x∈C и x∉B,
если x∉B, то (т.к. A⊂B) x∉A, имеем
x∈C и x∉A, => x∈C\A.
чтд.
11. Доказательство "⇒".
Пусть у нас дано (A∪B = A∩B), докажем тогда, что A = B.
Доказательсво. Пусть x∈A, тогда x∈AUB, но т.к. A∪B = A∩B, то
x∈A∩B, и т.к. A∩B⊂B, имеем x∈B. Мы доказали сейчас, что А⊂B.
Теперь докажем, что B⊂A. Доказательство аналогичное:
пусть x∈B, => x∈A∪B, т.к. A∪B = A∩B, то x∈A∩B, т.к. A∩B⊂A, => x∈A.
Итак, B⊂A.
Т.к. A⊂B и B⊂A, ⇔ A = B. чтд.
Доказательство "<=".
Пусть у нас дано A = B, докажем тогда, что A∪B = A∩B.
Если A = B, то A∪B = B∪B = B, и A∩B = B∩B = B,
то есть A∪B = B = A∩B.
12. Доказательство "=>"
Пусть у нас дано , докажем тогда, что
(A∩B = ∅) и (A∪B = U).
Доказательство. это по определению есть U\B, где U - универсальное множество, то есть у нас дано
A = U\B, тогда
A∩B = (U\B)∩B,
если x∈A∩B, то x∈A и x∈B, то есть x∈U\B и x∈B, то есть
x∈U и x∉B, и x∈B,
x не может одновременно и принадлежать B и не принадлежать B, то есть такого x не существует, то есть x∈∅, мы доказали, что A∩B ⊂∅, но тогда A∩B = ∅.
теперь докажем, что A∪B = U,
Очевидно, что A∪B ⊂U,
докажем, что U⊂A∪B (при условии ).
если x∈U, тогда x∈B или x∉B,
( если x∉B, тогда x∈ ), имеем
x∈B или x∈
но т.к.
имеем
x∈B или x∈A, то есть
x∈A∪B.
Мы доказали, что U⊂A∪B, и что A∪B⊂U (очевидное утверждение)
Итак, A∪B = U.
Пусть у нас дано: (A∩B = ∅) и (A∪B = U). Докажем, что
Доказательство. Пусть x∈A, при этом возможны два варианта:
x∈B или x∉B, то есть x∈B или x∈.
Если x∈B, тогда имеем x∈A∩B = ∅⊂
либо же x∈ и x∈A, ⇔ x∈A∩ ⊂,
то есть если x∈A => x∈
Пусть x∈, тогда x∈U\B, что значит x∈U и x∉B,
но т.к. U = A∪B, то имеем x∈A∪B и x∉B, то есть имеем
(x∈A или x∈B) и x∉B
если x∈A и x∉B, ⇔ x∈A\B ⊂ A, => x∈A,
если же x∈B и x∉B, то x∈∅ ⊂A, то есть x∈A,
итак ⊂A.
Мы доказали, что A⊂, и
.
10. У нас дано, что A⊂B.
Докажем, что (C\B)⊂(C\A).
Доказательство.
Пусть x∈C\B, тогда x∈C и x∉B,
если x∉B, то (т.к. A⊂B) x∉A, имеем
x∈C и x∉A, => x∈C\A.
чтд.
11. Доказательство "⇒".
Пусть у нас дано (A∪B = A∩B), докажем тогда, что A = B.
Доказательсво. Пусть x∈A, тогда x∈AUB, но т.к. A∪B = A∩B, то
x∈A∩B, и т.к. A∩B⊂B, имеем x∈B. Мы доказали сейчас, что А⊂B.
Теперь докажем, что B⊂A. Доказательство аналогичное:
пусть x∈B, => x∈A∪B, т.к. A∪B = A∩B, то x∈A∩B, т.к. A∩B⊂A, => x∈A.
Итак, B⊂A.
Т.к. A⊂B и B⊂A, ⇔ A = B. чтд.
Доказательство "<=".
Пусть у нас дано A = B, докажем тогда, что A∪B = A∩B.
Если A = B, то A∪B = B∪B = B, и A∩B = B∩B = B,
то есть A∪B = B = A∩B.
чтд.
12. Доказательство "=>"
Пусть у нас дано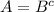 , докажем тогда, что
, докажем тогда, что
(A∩B = ∅) и (A∪B = U).
Доказательство. это по определению есть U\B, где U - универсальное множество, то есть у нас дано
это по определению есть U\B, где U - универсальное множество, то есть у нас дано
A = U\B, тогда
A∩B = (U\B)∩B,
если x∈A∩B, то x∈A и x∈B, то есть x∈U\B и x∈B, то есть
x∈U и x∉B, и x∈B,
x не может одновременно и принадлежать B и не принадлежать B, то есть такого x не существует, то есть x∈∅, мы доказали, что A∩B ⊂∅, но тогда A∩B = ∅.
теперь докажем, что A∪B = U,
Очевидно, что A∪B ⊂U,
докажем, что U⊂A∪B (при условии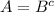 ).
).
если x∈U, тогда x∈B или x∉B,
( если x∉B, тогда x∈ ), имеем
), имеем
x∈B или x∈
но т.к.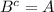
имеем
x∈B или x∈A, то есть
x∈A∪B.
Мы доказали, что U⊂A∪B, и что A∪B⊂U (очевидное утверждение)
Итак, A∪B = U.
Доказательство "<=".
Пусть у нас дано: (A∩B = ∅) и (A∪B = U). Докажем, что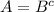
Доказательство. Пусть x∈A, при этом возможны два варианта:
x∈B или x∉B, то есть x∈B или x∈ .
.
Если x∈B, тогда имеем x∈A∩B = ∅⊂
либо же x∈ и x∈A, ⇔ x∈A∩
и x∈A, ⇔ x∈A∩  ⊂
⊂ ,
,
то есть если x∈A => x∈
Пусть x∈ , тогда x∈U\B, что значит x∈U и x∉B,
, тогда x∈U\B, что значит x∈U и x∉B,
но т.к. U = A∪B, то имеем x∈A∪B и x∉B, то есть имеем
(x∈A или x∈B) и x∉B
если x∈A и x∉B, ⇔ x∈A\B ⊂ A, => x∈A,
если же x∈B и x∉B, то x∈∅ ⊂A, то есть x∈A,
итак ⊂A.
⊂A.
Мы доказали, что A⊂ , и
, и
чтд.