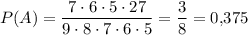1) (возьмем все задание за одну целую) 1 : 40 = 1/40 часть задания - выполнит первая бригада за один день, так как она может выполнить все задание за 40 дней;
2) 1 : 50 = 1/50 часть задания - выполнит вторая бригада за один день, так как она может выполнить все задание за 50 дней;
3) 1/40 + 1/50 = 5/200 + 4/200 = 9/200 части задания - могут выполнить две бригады за один день, работая вместе;
4) 1 : 9/200 = 1 * 200/9 = 200/9 = 22 2/9 дней - за такое время две бригады выполнят задание при совместной работе.
У нас есть 5 позиций: _ _ _ _ _. Посчитаем количество всех возможных на первую позицию можно поставить любую из 9 цифр, на вторую — любую из оставшихся 8, на третью — любую из оставшихся 7 и т. д., то есть всех возможных
Посчитаем количество подходящих На последней позиции должна быть нечётная цифра, на первой — 4, 5, 6 ... 9 (любая из них), а на остальных могут быть любые из оставшихся. Начнём с последней позиции: если мы поставим 1 или то на первую позицию можем поставить Тогда в этом случае подходящих Если на последнюю позицию поставим 5, 7 или то на первую позицию мы можем поставить только 5 цифр. И тогда подходящих Итого в обоих случаях 2·6·7·6·5 + 3·5·7·6·5 = 7·6·5·(2·6 + 3·5) = 7·6·5·27.
Решим данную задачу по действиям с пояснениями:
1) (возьмем все задание за одну целую) 1 : 40 = 1/40 часть задания - выполнит первая бригада за один день, так как она может выполнить все задание за 40 дней;
2) 1 : 50 = 1/50 часть задания - выполнит вторая бригада за один день, так как она может выполнить все задание за 50 дней;
3) 1/40 + 1/50 = 5/200 + 4/200 = 9/200 части задания - могут выполнить две бригады за один день, работая вместе;
4) 1 : 9/200 = 1 * 200/9 = 200/9 = 22 2/9 дней - за такое время две бригады выполнят задание при совместной работе.
ответ: не хватит, им нужно 23 дня.
0,375
Пошаговое объяснение:
У нас есть 5 позиций: _ _ _ _ _. Посчитаем количество всех возможных на первую позицию можно поставить любую из 9 цифр, на вторую — любую из оставшихся 8, на третью — любую из оставшихся 7 и т. д., то есть всех возможных
Посчитаем количество подходящих На последней позиции должна быть нечётная цифра, на первой — 4, 5, 6 ... 9 (любая из них), а на остальных могут быть любые из оставшихся. Начнём с последней позиции: если мы поставим 1 или то на первую позицию можем поставить Тогда в этом случае подходящих Если на последнюю позицию поставим 5, 7 или то на первую позицию мы можем поставить только 5 цифр. И тогда подходящих Итого в обоих случаях 2·6·7·6·5 + 3·5·7·6·5 = 7·6·5·(2·6 + 3·5) = 7·6·5·27.
Рассчитаем вероятность: