Для двух предприятий выделено a единиц средств. Как распределить все средства в течение 4 лет, чтобы доход был наибольшим, если известно, что доход от х единиц средств, вложенных в первое предприятие, равен f1(x), а доход от y единиц средств, вложенных во второе предприятие, равен f2(y). Остаток средств к концу года составляет g1(x) для первого предприятия и g2(y) для второго предприятия. Задачу решить методом динамического программирования.

ответ: х принадлежит промежутку(7; 7+^3√11), 7 –не входит в промежуток так как неравенство .строгое

Пошаговое объяснение:

До решения заданного неравенства решим уравнение вида

(x-7)^2 = корень из 11*(x-7)

Чтобы избавиться от квадратного корня возведем обе части уравнения в квадрат:

(х-7)^4=11(х-7),

х-7≥ 0, х≥ 7.

Переносим обе части уравнения в одну сторону :

(х-7)^4-11(х-7)=0

(х-7)((х-7)^3-11)=0

Составляем совокупность уравнений:

Х-7=0 или (х-7)^3-11=0

Х=7 или х=7+^3√11

Точки разделяют луч [7;+ ∞) на двапромежутка:

(7; 7+^3√11) и (7+^3√11; +∞), 2,2<^3√11<2,3

На первом промежутке (7; 7+^3√11)  исходное неравенство верно, на втором (7+^3√11; +∞) – неверно

, с точностью до перестановки.

Пошаговое объяснение:

Из уравнения

следует, что среди чисел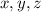 либо все нечетные, либо одно.

Заметим, что

Из нашего условия это преобразуется как

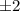Но мы знаем, что среди чисел либо все четные, либо одно. Если четны все, то они могут быть равны только в этом случае числа 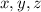могут быть равны с точностью до перестановки только 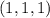или 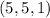. Второе решение не подходит в исходное уравнение, поэтому его отметаем. Если же среди чисел только одно четное, то оно обязано быть равно 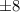, а остальные - 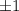. В этом случае 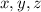равны 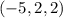, , 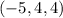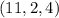. Из этих троек нам подходит только вторая.

В итоге, решений всего два.