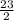a > 0 - ветви параболы направленны вверх
наименьшее значение достигается в вершине параболы:
Наименьшее значение достигается в точке и равно
a > 0 - ветви параболы направленны вверх
наименьшее значение достигается в вершине параболы:
Наименьшее значение достигается в точке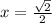 и равно
и равно