Для однофазного трансформатора с номинальной мощностью sном=8ква и номинальным напряжением u1ном=220в, используя данные опыта короткого замыкания: рк=600вт, uк=30в. определить активное реактивное и полное сопротивление тр-ра при коротком замыкании

1 сосуд 5 л 2 сосуд 7 л

Сначала наполняем полностью сосуд ёмкостью 7л. Потом выливаем воду в сосуд ёмкостью 5л и выливаем. Переливаем те 2 литра во 1 сосуд, которые остались в сосуде ёмкостью 7л. Набираем сосуд ёмкостью 7л. Переливаем 3 литра воды во 1 сосуд, так как там 2 литра. У нас получило что в сосуде ёмкостью 5л 5 л воды, а в сосуде ёмкостью 7 л 4 литра воды.

Выливаем из 1 сосуда воду и заливаем туда те 4 л воды. Тепер в сосуде ёмкостью 5 л 4 литра воды, а в сосуде ёмкостью 7 л нет воды.

Набираем сосуд ёмкостью 7 л воды полностью и выливаем в 1 сосуд 1 л воды, так как там уже есть 4 л воды. и во 2 сосуде ( ёмкостью 7 л) получилось 6 л

ДАНО: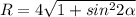 - функция, r = 4 - окружность,

НАЙТИ: Площадь фигуры вне окружности.²

Пошаговое объяснение - решение силой Разума.

Мысль 1. Задача в полярных координатах. Построение графика без использования дополнительных средств весьма затратно.

Рисунок с графиком функции при расчёте через 10° в приложении.

Мысль 2. Площадь фигуры - разность площадей функции и окружности с r= 4.

Мысль 3. Площадь окружности по формуле: S1 = π*r² = 16π - (запоминаем - потом надо вычесть).

Мысль 4. Площадь ограниченная функцией по формуле:

Пределы интегрирования от а = 0, до  b = 2π - запоминаем.

Мысль 5. Вычисляем значение R(α)²

R(α)² = 16*(1 + sin²2α).

Коэффициент 16 выносим из под интеграла и приступаем собственно к интегрированию.

Делаем подстановку - sin²x = (1-cos2x)/2 и получаем новый интеграл.

В результате получили функцию площади .

Вычисляем на границах интегрирования.

S2(2π) = 8*3π = 24π и S2(0) = 0 и

S2 - 24*π - площадь функции.

И переходим к ответу - вычитаем площадь центрального круга.

S = S2 - S1 =  24*π - 16*π = 8π (ед.²) - площадь фигуры - ответ.