для спортивной команды купили 304 майки и-209 футболок Найдите возможные наибольшее число спортсменов в команде если требуется чтобы каждый спортсмен получил одинаковый набор одежды и были использованы все вещи

для спортивной команды купили 304 майки и-209 футболок Найдите возможные наибольшее число спортсмено

Показать ответ

Ответ:

Kazybek0611

08.09.2020 19:57

Я выращиваю в доме мандарин. Когда я получил этот замечательный подарок, крона деревца была покрыта маленькими яркими мандаринчиками. К сожалению, при транспортировке растения из магазина много спелых плодов опало... Остальные мандаринчики я постепенно оборвал в течение месяца - когда они уже начали сохнуть. Но сразу удалять с деревца все спелые плоды мне не хотелось, ведь это было так красиво!Первое время мой мандарин был зелёный и бодрый. А потом, к концу первой зимы, у любимого деревца вдруг начали облетать листья и сохнуть ветки ... После первого же удобрительного полива «листопад» у моего мандарина прекратился, ветки тоже перестали сохнуть. Из-под земли рядом со стволом деревца выросли два маленьких побега, очень похожие внешне на ростки мандаринчиков; и листики у них такие же. Очень хочется их откопать и пересадить, но боюсь повредить корневую систему ...Когда мой мандарин в очередной раз набирает много-много бутонов и раскрывает свои цветочки, то стоит весь белый, словно снегом обсыпанный... Цветки мандарина очень ароматные, их запахом наполняется вся комната. А когда на домашнем цитрусовом деревце начинают зреть плоды, это для меня большой праздник!

0,0(0 оценок)

Ответ:

LetMaria

08.09.2020 19:57

1) Получаем треугольник AOB (см.рис1), стороны которого нам известны (AO=10 см, BO = 6 см, AB = 14 см). Из этого треугольника по теореме косинусов:

$\\AB^2=AO^2+BO^2-2\cdot AO\cdot BO\cdot\cos\hat{AOB}\Rightarrow\\\cos\hat{AOB}=\frac{AO^2+BO^2-AB^2}{2\cdot AO\cdot BO}=\frac{100+36-196}{2\cdot10\cdot6}=-\frac{60}{120}=-\frac12\Rightarrow\\AOB=\frac{2\pi}3=120^0$ .

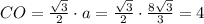
2) (см.рис2) Угол CDO - прямой, т.к. CD - расстояние от вершины С до грани угла (перпендикуляр). Значит, треугольник COD - прямоугольный, CO - гипотенуза. В то же время CO - высота равностороннего треугольника ABC. $\\CO=\frac{\sqrt3}2\cdot a=\frac{\sqrt3}2\cdot\frac{8\sqrt3}3=4$

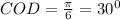
Из треугольника COD по определению синуса, синус угла COD равен отношению противолежащего катета CD к гипотенузе CO sinO= 2/4 = 1/2. То есть $COD=\frac{\pi}6=30^0$

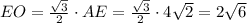
3) (см.рис3) В треугольнике EOF сторона EO - это высота равностороннего трегольника ABE $EO=\frac{\sqrt3}2\cdot AE=\frac{\sqrt3}2\cdot4\sqrt2=2\sqrt6$

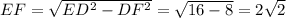Сторона OF равна стороне квадрата, DF равна половине стороны квадрата (OF - средняя линия ABCD), сторону EF найдём из прямоугольного треугольника EFD (EF перпендикуляр к CD => EFD - прямоугольный, ED - гипотенуза): $EF=\sqrt{ED^2-DF^2}=\sqrt{16-8}=2\sqrt2$ .

Тогда из треугольника EOF по тереме косинусов:

$\\EF^2=OE^2+OF^2-2\cdot OE\cdot OF\cdot\cos\hat{EOF}\Rightarrow\\\cos\hat{EOF}=\frac{OE^2+OF^2-EF^2}{2\cdot OE\cdot OF}=\frac{24+32-8}{2\cdot2\sqrt6\cdot4\sqrt2}=\frac{48}{16\sqrt{12}}=\frac{48}{32\sqrt3}=\frac{3}{2\sqrt3}=\frac{\sqrt3}2\\\Rightarrow \hat{EOF} = \frac{\pi}6=30^0$