До іть будь ласка з рішенням , по кроково 1. (1 3/7)^2=(1 3/7)х(1 3/7)=

2. (-2/3)^5

3. (-2,5)^2

4. (11/6)^2

5. (-1,1)^3

6. -(-0,5)^4

7. -(-3/4)^3

8. -(1,2)^2

Показать ответ

Ответ:

ЖақсыбаеваГүлзат

21.12.2020 19:06

Задача на знание формулы полной поверхности. она равна площади полной поверхности плюс две площади основания. Площадь основания равна произведению сторон на синус угла между ними. т.е.

6*8*0.5=24/м²/, площадь боковой поверхности равна произведению периметра основания на высоту, т.е. (6+8)*2*5=140, бок. ребро это высота, т.к. параллелепипед прямой.

Площадь полной поверхности равна 2*24+140=48+140=188/м²/

2. Высота конуса 5/2=2.5/м/, т.к. лежит против угла в 30°, она равна половине гипотенузы, коей является образующая, проекция образующей - радиус основания конуса, он равен 5*cos30°=2.5√3

Объем конуса равен (1/3)*πr²*h=(1/3)*π*6.25*3*2.5=15.625/м³/

Решить задачи 1) В прямом параллелепипеде стороны оснований 6м и 8м, а угол между ними 30 градусов.

0,0(0 оценок)

Ответ:

2001snk

23.05.2021 14:57

Сначала найдем общий вид первообразной для функции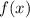 f(x) (здесь 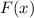F(x) - сама первообразная функция, производная которой равна 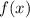f(x) , а 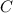- константа, которую хорошо было бы найти):

$\displaystyle F(x) \; = \; 5 \cdot \frac{x^2}{2} - 3 \cdot \frac{x^3}{3} + C \; = \; \frac {5x^2}{2} - x^3 + C$

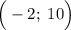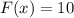Мы знаем, что график этой первообразной функции проходит через точку $\Big (-2 ; \; 10 \Big )$ . Это означает, что если мы подставим в получившееся равенство x=-2 , то получим F(x)=10 . Этим и воспользуемся, для того, чтобы отыскать константу:

$\displaystyle F(x) = \frac{5x^2}{2} - x^3 + C \\\\10 = \frac{5 \cdot (-2)^2}{2} - (-2)^3 + C\\\\10=10 + 8 + C \\\\8+C=0\\\\C = -8$

Несложно сделать вывод, что в этом случае уравнение первообразной будет следующим (и на всякий случай ниже предъявляю два графика - самой функции и ее первообразной, проходящей через заданную точку):

$\Large {\boxed { \displaystyle F(x) = \frac{5x^2}{2} - x^3 - 8} }$