Диаметр вписанной окружности в равнобедренной трапеции равен высоте этой трапеции. Соответственно h трапеции = 10 т.к. 2 радиуса.
Зная площадь трапеции можно найти её среднюю линию m = S/h = 115/10 = 11,5. Средняя линия есть сумма оснований трапеции делённая на 2. m = a+b/2. Если в трапецию можно вписать окружность, то сумма оснований такой трапеции = сумме боковых сторон. То есть в нашем случае c+d=a+b=m*2. Периметр трапеции = сумме всех сторон, P = a+b+c+d = m*2 + m*2 = 11,5 *4 = 46
46
Пошаговое объяснение:
Диаметр вписанной окружности в равнобедренной трапеции равен высоте этой трапеции. Соответственно h трапеции = 10 т.к. 2 радиуса.
Зная площадь трапеции можно найти её среднюю линию m = S/h = 115/10 = 11,5. Средняя линия есть сумма оснований трапеции делённая на 2. m = a+b/2. Если в трапецию можно вписать окружность, то сумма оснований такой трапеции = сумме боковых сторон. То есть в нашем случае c+d=a+b=m*2. Периметр трапеции = сумме всех сторон, P = a+b+c+d = m*2 + m*2 = 11,5 *4 = 46
1. А) x^2+5x-6<0
Х^2+6X-X-6 < 0
X*(X+6)-(X+6) < 0
(X+6)*(X-1) < 0
X ∈ ∅
X ∈ (-6,1)
б) 8x^2+24x ≥ 0
8Х*(Х+3) ≥ 0
Х*(Х+3)≥0
X∈ [0, + ∞)
X∈ ( -∞, -3]
B) x^2>4
|X| > 2
X>2, X≥0
-X>2, X<0
X∈(2, +∞)
X < -2, X < 0
X∈ ( 2, +∞)
X ∈ ( -∞, -2)
г) x^2-12x+36>0
(X-6)^2>0
(X-6)^2=0
X=6
2.
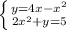
2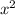
+4x - 
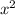= 5
x= -5
x= 1
y = 4*(-5) - (-5)^2
y = 4*1-1^2
y = -45
y = 3
(
, 
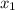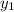) = (-5, -45)
(
, 
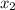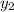) = (1, 3)
(
, 
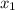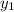) = (-5, -45)
(
, 
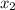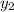) = (1,3)