Пошаговое объяснение:
Докажем гипотезу с метода математической индукции.
1. База индукции при кратно 19
2. Шаг индукции. Предположим, что при кратно 19. Докажем, что при при также будет кратно 19.
Уменьшаемое делится на 19, т.к. , а вычитаемое делится на 19, т.к. по предположению индукции делится на 19.
Следовательно и разность делится на 19.
Пошаговое объяснение:
Докажем гипотезу с метода математической индукции.
1. База индукции при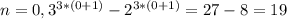 кратно 19
кратно 19
2. Шаг индукции. Предположим, что при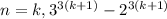 кратно 19. Докажем, что при при
кратно 19. Докажем, что при при  также будет кратно 19.
также будет кратно 19.
Уменьшаемое делится на 19, т.к.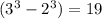 , а вычитаемое делится на 19, т.к. по предположению индукции
, а вычитаемое делится на 19, т.к. по предположению индукции  делится на 19.
делится на 19.
Следовательно и разность делится на 19.