Доказательство:
По неравенству Коши мы знаем, что среднее арифметическое не превышает среднее квадратичное, то есть выполняется следующее неравенство при неотрицательных a, b и с:
Так как , то имеем неравенство:
, что и требовалось доказать
Доказательство:
По неравенству Коши мы знаем, что среднее арифметическое не превышает среднее квадратичное, то есть выполняется следующее неравенство при неотрицательных a, b и с:
Так как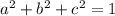 , то имеем неравенство:
, то имеем неравенство: