Дано: A(14;3); B(26;7); C(22;19); D(10;15).
Решение.
1) Найдём стороны четырёхугольника ABCD.
Стороны четырёхугольника ABCD равны между собой.
2) Найдём диагонали четырёхугольника ABCD.
Диагонали четырёхугольника ABCD равны между собой.
3) Если стороны четырёхугольника ABCD равны между собой и его диагонали равны между собой, значит, четырёхугольник ABCD - квадрат.
Доказано.
4) Найдём - площадь квадрата ABCD.
ответ:
Дано: A(14;3); B(26;7); C(22;19); D(10;15).
Решение.
1) Найдём стороны четырёхугольника ABCD.
Стороны четырёхугольника ABCD равны между собой.
2) Найдём диагонали четырёхугольника ABCD.
Диагонали четырёхугольника ABCD равны между собой.
3) Если стороны четырёхугольника ABCD равны между собой и его диагонали равны между собой, значит, четырёхугольник ABCD - квадрат.
Доказано.
4) Найдём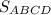 - площадь квадрата ABCD.
- площадь квадрата ABCD.
ответ: