143=11*13. Значит если число делится и на 11 и на 13 то оно делится и на 143, так как 11 и 13 простые. Нам нужно доказать что
Но если мы докажем что и , то мы докажем что 7^120-1 делится на 143.
Используем малую теорему ферма и получим что: .
Возведем обе части в натуральную степень 12 получим что
. То есть . Таким же образом доказывается для числа 13.
----------
Если что не понятно пишите
143=11*13. Значит если число делится и на 11 и на 13 то оно делится и на 143, так как 11 и 13 простые. Нам нужно доказать что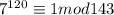
Но если мы докажем что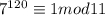 и
и 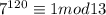 , то мы докажем что 7^120-1 делится на 143.
, то мы докажем что 7^120-1 делится на 143.
Используем малую теорему ферма и получим что: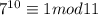 .
.
Возведем обе части в натуральную степень 12 получим что
----------
Если что не понятно пишите