Докажите, что числа a³ и b³ имеют одинаковый остаток - вопрос №10106883 от 260111092007 10.09.2021 23:24

Question

Математика: Докажите, что числа a³ и b³ имеют одинаковый остаток при делении на a - b. учтите: a³ ≡ m (mod a - b) ⇔ a³ = q1 * (a - b) + m ⇔ a³ / (a - b) = q1 + m / (a - b) b³ ≡ m (mod a - b) ⇔ b³ = q2 * (a - b) + m ⇔ b³ / (a - b) = q2 + m / (a - b)

260111092007 · Answer

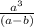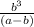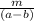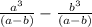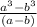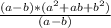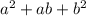
Если и имеют одинаковый остаток m, то дробная часть результата деления равна  , и их разность будет целым числом.Но их разность равна = = = что является целым числом, следовательно, остаток одинаковый....