1) При равенство примет вид , следовательно, при имеем верное равенство.
2) Предположим справедливость этого утверждения для , где — произвольное натуральное число, и с учетом этого предположения установим справедливость для
Следовательно, при имеем истинное утверждение.
3) Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального .
1) При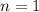 равенство примет вид
равенство примет вид 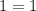 , следовательно, при
, следовательно, при 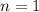 имеем верное равенство.
имеем верное равенство.
2) Предположим справедливость этого утверждения для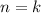 , где
, где 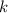 — произвольное натуральное число, и с учетом этого предположения установим справедливость для
— произвольное натуральное число, и с учетом этого предположения установим справедливость для 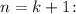
Следовательно, при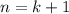 имеем истинное утверждение.
имеем истинное утверждение.
3) Таким образом, согласно методу математической индукции, исходное равенство справедливо для любого натурального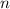 .
.