Условие не является полным. Это известное неравенство так называемое неравенство Бернулли и оно гласит, что для имеет место неравенство
1) При база индукции выполнено:
2) Предположим, что для имеет место неравенство
3) Докажем, что
Неравенство верно из предположения 2). Утверждение доказано.
Условие не является полным. Это известное неравенство так называемое неравенство Бернулли и оно гласит, что для имеет место неравенство
имеет место неравенство 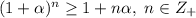
1) При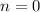 база индукции выполнено:
база индукции выполнено: 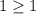
2) Предположим, что для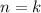 имеет место неравенство
имеет место неравенство
3) Докажем, что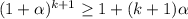
Неравенство верно из предположения 2). Утверждение доказано.