Войти
Регистрация
Спроси ai-bota
В
Все
М
Математика
О
ОБЖ
У
Українська мова
Д
Другие предметы
Х
Химия
М
Музыка
Н
Немецкий язык
Б
Беларуская мова
Э
Экономика
Ф
Физика
Б
Биология
О
Окружающий мир
Р
Русский язык
У
Українська література
Ф
Французский язык
П
Психология
А
Алгебра
О
Обществознание
М
МХК
В
Видео-ответы
Г
География
П
Право
Г
Геометрия
А
Английский язык
И
Информатика
Қ
Қазақ тiлi
Л
Литература
И
История
Показать больше
Показать меньше
uliamykytyn
27.11.2020 19:27 •
Математика
Докажите тождество если то
Показать ответ
Ответ:
Gurza97
04.09.2020 22:33
.
.
.
.
Откуда
.
0,0
(0 оценок)
Популярные вопросы: Математика
Алика666
02.03.2021 04:14
Какая схема подходит для решения задачи в городе школа в 3 раза больше чем детсадов всего в городе 128 школы десадов сколько школы Сколько детсада в городе УМОЛЯЮ ...
kudadiana3101
06.06.2021 08:26
Найдите в справочной литературе, школьных учебников по другим предметам, переодической печать или Интернете примеры применения процентов. Составьте задачу на проценты и решите...
ruskei
13.11.2022 21:48
1.Сократить дробь a^2+2a+1/a^-1 при a = -0.5; 1/3; 3; -1/3; -3...
vi600081
20.03.2021 10:57
С 1 по 5 от этого зависит мои отметки ...
shaduraalya
04.06.2023 16:58
Очень . Оценка идёт в диплом...
агенбенди003
14.08.2020 01:21
Туристи пройшли 16 км,що становить 80% усього маршуту.Знайдіть довжину усього маршуту...
zhovnovich
28.07.2020 18:48
1.Длина шага школьника 6 дм. Сколько ему нужно сделать ша- гов, чтобы пройти 6 метров?9. Юра хотел умножить какое-то число на7. При умножении оношибся и получил число 540, что...
Ariana030709
05.02.2022 04:59
3(у-2)+2(у+1)-8при у очень...
polina3782
30.07.2021 13:26
Побудуй гоадусну миру 110° и цого бисектрису...
WaterdropE
27.11.2022 00:55
Найдите значение k:l если известно что m:n=38 и m:k=2 n:l...
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Откуда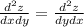 .
.