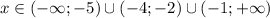1) Сначала переведем в одну меру длины. Предлагаю в сантиметры. В 1 м = 100 см. Тогда, длина самого большого куска ткани равна 9 м = 900 см - это первый кусок.
2) Второй кусок, который меньше на 150 см(1м 50 см) = 900 см - 150 см = 750 см (7м50см)
3)Третий кусок. Если он короче предыдущего, то 750 см -150 см = 600 см (6м)
4)Четвертый кусок. Также короче предыдущего, то есть 600 см -150 см = 450 см (4м 50см)
5)Теперь найдём длину всего рулона, просто сложив всё:
900 см + 750 см + 600 см + 450 см = 2700 см (27м).
Приравняем неравенство к нулю и найдем нули множителей:
Перепишем многочлены вида на множители вида , где и — корни квадратного уравнения
Имеем:
Начертим координатную прямую и отметим выколотыми точками (так как неравенство строгое) нули множителей, и определим знак на каждом интервале ("+", если на этом интервале функция выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.
Следовательно, промежутками, на которых функция больше нуля (выше оси абсцисс), являются:
Неравенство вида выполняется в двух случаях:
Следовательно, рассмотрим первый случай:
Здесь и — точки пересечения графика функции с осью абсцисс, и и — точки пересечения графика функции с осью абсцисс.
Изобразим две параболы для каждого неравенства и определим те абсциссы, при которых каждая из них больше нуля (см. вложение). Имеем промежутки:
Следовательно, промежутками, при которых оба неравенства выполняются одновременно, являются:
Рассмотрим второй случай:
Из тех же парабол определим те абсциссы, при которых каждая из них меньше нуля:
Следовательно, промежутком, при котором оба неравенства выполняются одновременно, является:
Объединим оба случая и получим решение неравенства:
Відповідь:
2700см(27м)
Покрокове пояснення:
1) Сначала переведем в одну меру длины. Предлагаю в сантиметры. В 1 м = 100 см. Тогда, длина самого большого куска ткани равна 9 м = 900 см - это первый кусок.
2) Второй кусок, который меньше на 150 см(1м 50 см) = 900 см - 150 см = 750 см (7м50см)
3)Третий кусок. Если он короче предыдущего, то 750 см -150 см = 600 см (6м)
4)Четвертый кусок. Также короче предыдущего, то есть 600 см -150 см = 450 см (4м 50см)
5)Теперь найдём длину всего рулона, просто сложив всё:
900 см + 750 см + 600 см + 450 см = 2700 см (27м).
Метод интервалов.
Приравняем неравенство к нулю и найдем нули множителей:
Перепишем многочлены вида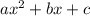 на множители вида
на множители вида 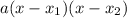 , где
, где 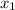 и
и 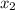 — корни квадратного уравнения
— корни квадратного уравнения 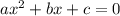
Имеем:
Начертим координатную прямую и отметим выколотыми точками (так как неравенство строгое) нули множителей, и определим знак на каждом интервале ("+", если на этом интервале функция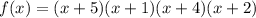 выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.
выше оси абсцисс, "–" — ниже оси абсцисс). См. вложение.
Следовательно, промежутками, на которых функция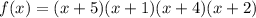 больше нуля (выше оси абсцисс), являются:
больше нуля (выше оси абсцисс), являются:
Неравенство вида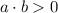 выполняется в двух случаях:
выполняется в двух случаях:
Следовательно, рассмотрим первый случай:
Здесь и
и 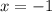 — точки пересечения графика функции
— точки пересечения графика функции 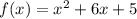 с осью абсцисс, и
с осью абсцисс, и 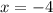 и
и  — точки пересечения графика функции
— точки пересечения графика функции 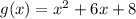 с осью абсцисс.
с осью абсцисс.
Изобразим две параболы для каждого неравенства и определим те абсциссы, при которых каждая из них больше нуля (см. вложение). Имеем промежутки:
Следовательно, промежутками, при которых оба неравенства выполняются одновременно, являются:
Рассмотрим второй случай:
Из тех же парабол определим те абсциссы, при которых каждая из них меньше нуля:
Следовательно, промежутком, при котором оба неравенства выполняются одновременно, является:
Объединим оба случая и получим решение неравенства:
ответ: