Цифрам буду давать номера слева на право (1ая - самая левая).
Максимально возможная первая цифра это 6, т.к. после неё больше будут только 7, 8, 9, всего 3.
Каждая следующая цифра (для первых 4) меньше предыдущей т.к. должны использоваться все цифры, а если следующая будет больше, то не получится "3333", будет "321...". 5ая цифра должна быть больше 1ой, чтобы сбросилось кол-во больших цифр с 3 до 2. Аналогично недавним рассуждениям, 6ая и 7ая цифра должны быть меньше предыдущей, при этом 6ая меньше 4ой. Далее 8ая больше 5ой. 9ая меньше 7ой. 10ая больше 8ой.
Мы получили, что после 1ой цифры должно быть 6 цифр, которые меньше её. Наименьшая возможная цифра это 6 т.к. меньше её 5, 4, 3, 2, 1, 0, всего 6.
Максимальное и минимальное значение для первой цифры это 6, значит первая цифра именно 6. После рассуждений, приведённый выше, получим число.
Пошаговое объяснение:
1.1 Прочертим диагональ и получим треугольник со сторонами 8,3 и углом между ними 120°
По теореме косинусов можем вычислить диагональ(третью сторону)
a²=b²+c²-2bc*cos120
a²=64+9-2*8*3*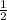
a²=49
a=7
Диагональ равна 7
1.2 Sпараллелограмма=h*a
Проведем высоту к сторону равной 8
угол между высотой и меньшей стороной будет 120-90=30, а значит мы получаем прямоугольный треугольник с углом в 30° и гипотенузой равной 3
Следовательно сторона напротив угла в 30°=3/2=1,5
По теореме Пифагора находим высоту
9=h²+2,25
h=2,5
Sпараллелограмма=2,5*8=20
2. Тут понадобится теорема синусов
(8√2)/(sin45)=(8√3)/(sinx)
sin45=√2/2
(8√2)/(√2/2)=16 ⇒ (8√3)/(sinx)=16
sinx=(8√3)/16=√3/2
sinx=√3/2 ⇒ x=60°
∠D=60°
3. Sсектора=(πR²*α)/(360)
В правильном шестиугольнике a=R⇒R=6
α=60
Sсектора=(36*60π)/(360)
Sсектора=6π≈18,84
4. АВ=√18
BC=√((-1-(-5))²+(-5-(-1))²)=√32
СD=√18
AD=√((2-(-2)²+(-2-2)²)=√32
Из этих вычислений следует то, что ABCD параллелограмм
Если AC²=AB²+BC²=AD²+CD² ,то ABCD прямоугольник
AC=√50
(√50)²=(√18)²+(√32)²
50=18+32⇒ABCD прямоугольник
5. Уравнение окружности это
(x-xцентра)²+(y-yцентра)²=R²
(x+7)²+(y-1)²=81
Центр окружности в точке (-7;1); R=9
При параллельном переносе на {3;-8} центр окажется в точке (-4;-7); радиус не изменится, значит уравнение будет выглядить вот так
(x+4)²+(y+7)²=81
Главное, что были использованы все цифры!
Цифрам буду давать номера слева на право (1ая - самая левая).
Максимально возможная первая цифра это 6, т.к. после неё больше будут только 7, 8, 9, всего 3.
Каждая следующая цифра (для первых 4) меньше предыдущей т.к. должны использоваться все цифры, а если следующая будет больше, то не получится "3333", будет "321...". 5ая цифра должна быть больше 1ой, чтобы сбросилось кол-во больших цифр с 3 до 2. Аналогично недавним рассуждениям, 6ая и 7ая цифра должны быть меньше предыдущей, при этом 6ая меньше 4ой. Далее 8ая больше 5ой. 9ая меньше 7ой. 10ая больше 8ой.
Мы получили, что после 1ой цифры должно быть 6 цифр, которые меньше её. Наименьшая возможная цифра это 6 т.к. меньше её 5, 4, 3, 2, 1, 0, всего 6.
Максимальное и минимальное значение для первой цифры это 6, значит первая цифра именно 6. После рассуждений, приведённый выше, получим число.
ответ: 6543721809.