Два товара в сумме стоят 4 руб.если стоимость 1 меньше на 10% а второго на 40 вместе не будут стоить 3,3 руб.найдите(в рублях)стоимость товара для изменения цен
В условии задачи не сказано, могут ли цифры повторяться. Но нам всё равно не подходят числа, составленные из двух одинаковых цифр. Ведь сумма цифр любого такого числа будет четной. Поэтому мы будем считать, что цифры не должны повторяться.
Составим все возможные двузначные числа из цифр ноль, один, два и три. Также найдем сумму цифр каждого составленного числа.
1. Пусть первая цифра двузначного числа - это цифра один.
Мы можем составить следующие числа: 10; 12; 13.
Сумма цифр числа 10 равна единице. Единица - нечетное число.
Сумма цифр числа 12 равна трем. Три - нечетное число.
Сумма цифр числа 13 равна четырем. Четыре - четное число.
2. Пусть первая цифра двузначного числа - это цифра два.
Мы можем составить следующие числа: 20; 21; 23.
Сумма цифр числа 20 равна двум. Два - четное число.
Сумма цифр числа 21 равна трем. Три - нечетное число.
Сумма цифр числа 23 равна пяти. Пять - нечетное число.
3. Пусть первая цифра двузначного числа - это цифра три.
Мы можем составить следующие числа: 30; 31; 32.
Сумма цифр числа 30 равна трем. Три - нечетное число.
Сумма цифр числа 31 равна четырем. Четыре - четное число.
Сумма цифр числа 32 равна пяти. Пять - нечетное число.
Берём, скажем, точку как отправную, и размножаем векторы и , используя параметры и :
Отсюда параметрические уравнения:
Неявное уравнение
В уравнении коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
Найдём вектор нормали как векторное произведение векторов и :
Итого
Предварительный вид неявного уравнения:
Найдём D, подставив какую-нибудь из точек из условия, скажем, С:
9
Пошаговое объяснение:
Составим двузначные числа из данных цифр
В условии задачи не сказано, могут ли цифры повторяться. Но нам всё равно не подходят числа, составленные из двух одинаковых цифр. Ведь сумма цифр любого такого числа будет четной. Поэтому мы будем считать, что цифры не должны повторяться.
Составим все возможные двузначные числа из цифр ноль, один, два и три. Также найдем сумму цифр каждого составленного числа.
1. Пусть первая цифра двузначного числа - это цифра один.
Мы можем составить следующие числа: 10; 12; 13.
Сумма цифр числа 10 равна единице. Единица - нечетное число.
Сумма цифр числа 12 равна трем. Три - нечетное число.
Сумма цифр числа 13 равна четырем. Четыре - четное число.
2. Пусть первая цифра двузначного числа - это цифра два.
Мы можем составить следующие числа: 20; 21; 23.
Сумма цифр числа 20 равна двум. Два - четное число.
Сумма цифр числа 21 равна трем. Три - нечетное число.
Сумма цифр числа 23 равна пяти. Пять - нечетное число.
3. Пусть первая цифра двузначного числа - это цифра три.
Мы можем составить следующие числа: 30; 31; 32.
Сумма цифр числа 30 равна трем. Три - нечетное число.
Сумма цифр числа 31 равна четырем. Четыре - четное число.
Сумма цифр числа 32 равна пяти. Пять - нечетное число.
Параметрические уравнения:
Неявное уравнение:
Пошаговое объяснение:
Параметрическое уравнение
Вектор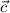 :
:
Вектор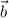 :
:
Берём, скажем, точку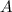 как отправную, и размножаем векторы
как отправную, и размножаем векторы 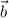 и
и 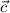 , используя параметры
, используя параметры  и
и 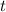 :
:
Отсюда параметрические уравнения:
Неявное уравнение
В уравнении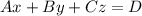 коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
коэффициенты A, B, C - это координаты вектора нормали, а D - коэффициент, сдвигающий плоскость, задаваемую вектором нормали, так, чтобы плоскость содержала в себе одну из точек из условия.
Найдём вектор нормали как векторное произведение векторов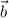 и
и 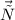 :
:
Итого
Предварительный вид неявного уравнения:
Найдём D, подставив какую-нибудь из точек из условия, скажем, С:
Итого: