Две закон распределения дискретной случайной величины
1) найти вероятность p
2) найти функцию распределения f(x) и построить ее график
3) вычислить m (x), d (x), a (x)

3584

Пошаговое объяснение:

Пусть в сборнике n задач, тогда:

За 1 день решено: n/2+1

За 2 день решено: n/4+2

За 3 день решено: n/8+3

...

За 7 день решено: n/2^7+7

Сложим решенные за все дни задачи, причём дроби вида n/2^k (k - от 1 до 7) отделим от вторых слагаемых каждого дня:

(n/2+n/4+...+n/256)+(1+2+...+7)=n

Вынесем n из первой скобки:

n*(1/2+1/4+...+1/256)+(1+2+...+7)=n

Первая скобка (без n) - сумма первых семи членов геометрической прогрессии со знаменателем 1/2.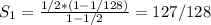

Вторая скобка - сумма первых семи членов арифметической прогрессии с разностью 1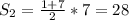

Мячей - 13, скакалок - 1, обручей - 1

Пошаговое объяснение:

Пусть тренер купил x скакалок, y обручей, z мячей, тогда:

260x+130y+100z=1690, причём x,y,z - целые числа (такие уравнения называются диофантовы)

Вынесем 130 из певрых двух слагаемых

130(2x+y)+100z=1690

Исходя из того, что ответ должен быть целым числом значение 2x+y равно 3, т.к только при умножении на 3 мы сможем получить в ответе 9 десятков.

Далее, 2x+y=3, значит в натуральных числах ответ единственен: x=1; y=1

Подставим значения x,y и найдём z:

390+100z=1690

100z=1300

z=13