Екую европу с азией, продвинуло человечество к удивительным достижениям, оказав положительное влияние на взаимную торговлю развитых стран, на развитие отраслей нау
это как делать

ну, в первой загадке вы опечатались в условии, похоже:

должно быть так: "через точку а к окружности w (0,r)проведены". а то выходит, что а принадлежит окружности, при этом через нее аж две касательные

ну а доказывать, полагаю, надо через равенство треугольников, образующихся при соединении этой точки а с центром окружности и радиусов, проведенных к точкам касания в и с.

треугольники аво и асо:

во-первых, прямоугольные. (углы в и с прямые, ибо радиус к точке касания перперндикулярен касательной);

во-вторых, имеют равные катеты ов и ос (длина их - радиус окружности);

в-третьих - у них равные гипотенузы (она у них общая, это отрезок ао);

значит они равны (по углу и двум сторонам)

следовательно ав=ас.

согласны?

а вот что думаю про вторую :

раз угол прямой, то, соединив отрезками точки касания с центром окружности, получим симпатичный квадрат, диагональ которого - та самая хорда.

ну, а у квадрата диагонали равны и перпендикулярны друг другую.

значит проводим вторую диагональ (она как раз из центра к хорде под прямым углом пойдет) и сразу становится видно, что расстояние от хорды то центра окружности окружности - ровно половина диагонали, т.е.

40/2 = 20см

ура?

))

Представить число 7 в виде суммы трех натуральных слагаемых можно следующими с точностью до порядка слагаемых):

Представления первыми двумя не могут соответствовать  сторонам треугольника, так как для них не выполняется неравенство треугольника. Заметим, что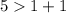 и 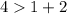, хотя каждая сторона треугольника должна быть меньше суммы двух других сторон.

Значит, треугольник имеет стороны 1, 3, 3 или 2, 2, 3. Каких-либо других ограничений на сторону АВ нет, поэтому она может иметь длину 1, 2 или 3.

ответ: 1, 2 или 3