Половину пути принимаем за 1, тогда весь путь - 2. Пусть скорость первого автомобилиста равна х км/ч, тогда скорость второго на второй половине пути равна (х+9) км/ч. Первый был в пути 2/х часов, второй - 1/30 + 1/(х+9) часов. Зная, что их время одинаковое, составляем уравнение. 2/х = 1/30 + 1/ (х+9)
Приводим к общему знаменателю и приравниваем числители. 60(х+9) = х²+9х+30х х²+39х-60х-540=0 х²-21х-540=0 D=441+2106=2601 √D=51 х₁=(21-51)/2=-15 - не подходит по условию задачи х₂=(21+51)/2 = 36
Пусть скорость первого автомобилиста равна х км/ч, тогда скорость второго на второй половине пути равна (х+9) км/ч.
Первый был в пути 2/х часов, второй - 1/30 + 1/(х+9) часов. Зная, что их время одинаковое, составляем уравнение.
2/х = 1/30 + 1/ (х+9)
Приводим к общему знаменателю и приравниваем числители.
60(х+9) = х²+9х+30х
х²+39х-60х-540=0
х²-21х-540=0
D=441+2106=2601
√D=51
х₁=(21-51)/2=-15 - не подходит по условию задачи
х₂=(21+51)/2 = 36
ответ. 36 км/ч скорость первого автомобилиста.
Пусть
- это наименьшее число вращений первой шестеренки с 51 зубчиками;
а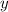
- это наименьшее число вращений второй шестеренки с 34 зубчиками.
До первоначального положения
первая шестеренка прокрутит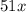
зубчиков,
а вторая прокрутит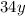
зубчиков.
Получаем уравнение:
Так как
- натуральное число, значит, дробь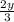 
должна быть натуральным числом, но это возможно если значения 
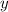будут кратны 3, т.е. при 
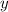= 3; 6 ; 9; 12; ...
Нам нужно минимальное значение!
При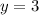
ответ: через 2 вращения большой шестеренки обе шестеренки встанут в первоначальное положение.