Математика: Если порабыла переходящий на точке А(2:0) Найдите

Если порабыла переходящий на точке А(2:0) Найдите

Показать ответ

Ответ:

hjccbyfoyf6ui

03.12.2022 12:16

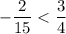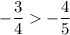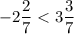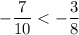
1. и) $\displaystyle -\frac{2}{15}$ ; к) $\displaystyle -\frac{3}{4} -\frac{4}{5}$ ; $\displaystyle -2\frac{2}{7}$ ; л) $\displaystyle -\frac{7}{10}$

2. Точки построены. См. рисунок.

Пошаговое объяснение:

Требуется сравнить числа и записать их в виде неравенства. Также, приняв за единичный отрезок длину 6 клеток тетради, начертить координатную прямую и отметить на ней точки.

1. Сравним числа:

и)

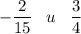
$\displaystyle - \frac{2}{15}\;\;\; u\;\;\;\frac{3}{4}$

Отрицательное число всегда меньше положительного.

$\displaystyle -\frac{2}{15}$

к)

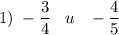
$\displaystyle 1)\;-\frac{3}{4} \;\;\;u\;\;\;-\frac{4}{5}$

Чтобы сравнить две дроби с разными знаменателями, надо вначале привести их к общему положительному знаменателю, а затем сравнить.

Используем основное свойство дроби:

Если числитель и знаменатель дроби умножить или разделить на одно и тоже число, получим дробь, равную данной.

Приведем дроби к общему знаменателю 20:

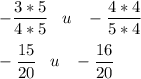
$\displaystyle -\frac{3*5}{4*5}\;\;\;u\;\;\;-\frac{4*4}{5*4}\\ \\ -\frac{15}{20} \;\;\;u\;\;\;-\frac{16}{20}$

Из двух отрицательных чисел больше то, у которого модуль меньше.

Также вспомним:

Модуль положительного числа - само число, а модуль отрицательного - число, противоположное данному.

Сравним модули чисел:

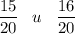
$\displaystyle \frac{15}{20}\;\;\;u\;\;\;\frac{16}{20}$

Из двух дробей с общим положительным знаменателем больше та, у которой больше числитель.

$\displaystyle \frac{15}{20}$

Следовательно:

$\displaystyle - \frac{15}{20}-\frac{16}{20}$ или $\displaystyle -\frac{3}{4} -\frac{4}{5}$

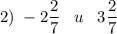
$2) \displaystyle \; -2\frac{2}{7}\;\;\;u\;\;\;3\frac{2}{7}$

Отрицательное число всегда меньше положительного.

$\displaystyle -2\frac{2}{7}$

л)

$\displaystyle -\frac{7}{10} \;\;\;u\;\;\;-\frac{3}{8}$

Приведем дроби к общему знаменателю 40, пользуясь основным свойством дроби:

$\displaystyle -\frac{7*4}{10*4} \;\;\;u\;\;\;-\frac{3*5}{8*5}\\\\\displaystyle -\frac{28}{40} \;\;\;u\;\;\;-\frac{15}{40}$

Сравним модули этих дробей:

$\displaystyle \frac{28}{40} \frac{15}{40}$

Следовательно:

$\displaystyle -\frac{28}{40}$ или $\displaystyle -\frac{7}{10}$

2. Начертим числовую ось и отметим единичный отрезок 6 клеток.

Если наш единичный отрезок 6 клеток, то одна клеточка будет равна одной шестой части.

Воспользуемся основным свойством дроби.

Данные дроби, у которых знаменатель отличный от 6, приведем к знаменателю 6.

Затем отметим эти числа на числовой оси.

$\displaystyle K\left(\frac{1}{3} \right)\\\\\frac{1}{3}=\frac{1*2}{3*2}=\frac{2}{6}$

$\displaystyle C\left(-0,5\right)\\\\-0,5=-\frac{1}{2}=-\frac{1*3}{2*3}=-\frac{3}{6}$

$\displaystyle D\left(-1\frac{1}{3}\right)\\\\-1\frac{1}{3}=-1\frac{1*2}{3*1}=-1\frac{2}{6}$

$\displaystyle E\left(\frac{1}{6}\right)$

$\displaystyle F\left(1\frac{1}{6}\right)$

$\displaystyle A\left(-\frac{5}{6}\right)$

$\displaystyle B\left(\frac{2}{3}\right)\\\\\frac{2}{3}=\frac{2*2}{3*2}=\frac{4}{6}$

$\displaystyle R\left(-\frac{1}{6}\right)$

$\displaystyle M\left(1,5\right)\\\\1,5=1\frac{1}{2}=1\frac{1*3}{2*3}=1\frac{3}{6}$

Отметим точки на числовой оси:

1) сравните числа и результат запишите в виде неравенства и) -2/15 и 3/4 к) -3/4 и -4/5; -2 2/7 и 3

0,0(0 оценок)

Ответ:

artemhkolnik

19.04.2022 03:14

Предложим, что основание равнобедренного треугольника = 7 см, значит, боковые стороны равны (из определения равнобедренного треугольника "Равнобедренный треуголник - это треугольник, у которого боковые стороеы равны"), найдем их.19 - 7 = 12 см. 12:2 = 6 см.

Вспомним "Неравенство треугольников". Каждая сторона треугольника меньше суммы двух других сторон. Возьмем треугольник АВС, например (прикреплен к ответу). Проверяем.

AB < AC+BC AC > AB+BC ВС < AB+AC

6 см < 13 см 7 см < 12 см 6 см < 13 см

Мы доказали, что такой треугольник существует.

ответ: основание = 7 см, боковые стороны = по 6 см каждая.

0,0(0 оценок)

Популярные вопросы: Математика