Математика: Если s(z)=z10−9,то s(−4) = .

Если s(z)=z10−9,

то s(−4) = .

Показать ответ

Ответ:

julija74

25.12.2022 12:39

Если рассматривать числа с разными цифрами, то:
Десятичная запись такого числа имеет вид: 10*Х+У.
При делении на Х получаем 10+У/Х - целое.
Значит У/Х - целое. Обозначим его к. Тогда У=к*Х.
Значит число имеет вид 10*Х+к*Х.
При делении на У=к*Х получаем (10+к) /к=10/к+1 - целое.
Значит 10/к - целое, к может быть равно или 2 или 5.
При к=5 Х может быть только 1, а У=5, т. е число 15.
При к=2 Х может принимать значения 1, 2, 3, 4.
Это числа 12, 24, 36, 48.
Если рассматривать числа с одинаковыми цифрами, то это могут быть 11, 22, 33, 44, 55, 66, 77, 88, 99.
Но скорее всего имеются в виду числа с разными цифрами: 12, 15, 24, 36, 48.

0,0(0 оценок)

Ответ:

Пакета

09.05.2021 03:37

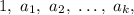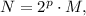Пусть N имеет натуральные делители $1,\ a_1,\ a_2,\ \ldots,\ a_k,$ и их сумма равна A. Пусть, кроме того, $N=2^p\cdot M,$ где N - нечетное число.

Четные делители числа N имеют вид

$2,\ 2a_1,2a_2,\ \ldots, 2a_k;\ 2^2,\ 2^2a_1,\ \ldots,\ 2^2a_k;\ldots;\ 2^p,\ 2^pa_1,\ \ldots,\ 2^pa_k.$

Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим

$2(1+a_1+\ldots+a_k)+2^2(1+a_1+\ldots+a_k)+\ldots + 2^p(1+a_1+\ldots +a_k)=$

$=2A+2^2A+\ldots 2^pA=2A\frac{2^p-1}{2-1}=2A(2^p-1).$

Требуется проверить, может ли

$A\cdot2A(2^p-1)+1=2A^2(2^p-1)+1$

быть полным квадратом, то есть равняться B².

Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы

2a^2(2^p-1)=B^2-1=(B-1)(B+1).

Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.

0,0(0 оценок)

Популярные вопросы: Математика