Если в ответе десятичная дробь то запишите её через запятую если в ответе обыкновенная дробь то запишите её в несократимом виде через черту/ если в ответе смешанная дробь то запишите целую часть через пробел от дробной -5 1/2
7= %
0,8.= %
600= %
40=. %
ответ: y(3)=0 .
Чтобы построить прямую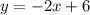
, надо знать координаты двух любых точек .
Необходимо задать одной переменной, например, переменной "х" произвольное числовое значение, и подставив это число в уравнение прямой, вычислить значение второй переменной "у" .
Так как в условии спрашивают, чему будет равно значение функции при х=3, то вычислим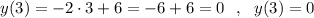
.
Пусть теперь х=2, тогда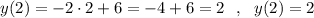
.
Построим прямую, проходящую через две точки: А(3;0) и В(2;2) .
Заметь, что при х=0 получим у=6, то есть точка пересечения с осью ОУ - это точка (0;6) . И число 6 в уравнении прямой у= -2х+6 является свободным членом .
ответ: 334
Пошаговое объяснение:
Все ждал пока детки добавят решение, но ладно уж, добавлю сам.
Как я понял, в условии предполагается, что числа должны быть различны, ибо возникает деление на 0.
Предположим, что в таком наборе существуют два числа a и b (a>b), разность которых равна 1, но тогда a+b делится на a-b, ибо a-b = 1.
Мы пришли к противоречию, такое невозможно.
Предположим теперь, что в таком наборе существует два числа a и b (a>b), разность которых равна 2. Два числа, разность которых равна 2 имеют одинаковую четность, а значит их сумма a+b является четной, то есть делится на их разность a-b = 2.
Мы пришли к противоречию, такое невозможно.
Таким образом, если данный набор упорядочить в порядке возрастания, то разность между соседними числами в данном наборе не менее 3.
Пусть в данном наборе n членов, тогда с учетом вышесказанного должно выполняться неравенство:
1+3(n-1) <=1000
3(n-1)<=999
n-1 <=333
n<=334
То есть в таком ряду не более 334 членов.
Покажем набор с 334 членами.
Возьмем все числа, что при делении на 3 дают остаток 1 и не более 1000:
1,4,7,10,13..., 1000 = 1+3*333 , то есть как раз 334 числа.
Возьмем любые два числа a и b (a>b) из данного набора.
Поскольку числа a и b дают при делении на 3 остаток 1, то их сумма a+b дает при делении на 3 остаток 2, то есть не делится на 3, однако их разность a-b дает при делении на 3 остаток 0, то есть делится на 3, а значит сумма a+b не может делится на разность a-b, то есть данный набор удовлетворяет условию задачи.