Математика: если x-число между 11,3 и 15, 993

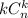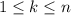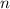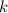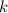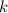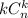Рассмотрим слагаемое , .Это количество сочетаний из элементов по , повторенное столько же раз.Выстроим одну из комбинаций из элементов в строчку. Домножив на , получим квадрат элементов. То есть — это множество квадратов. Теперь построим квадратную таблицу 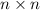(см.рис)В первой строке будут первые строчки большинства квадратов, кроме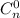 . Во второй строчке уже не будет 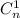, поскольку квадраты 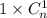целиком умещаются в первой строчке. И т.д. Причем будет отсутствовать вычитаемое , т.к. этот квадрат содержит все строчки....

если x-число между 11,3 и 15, 993

Показать ответ

Ответ:

malikamalik1406

17.05.2021 09:54

Рассмотрим слагаемое $kC_{n}^{k}$ , $1\leq k\leq n$ .

Это количество сочетаний из элементов по , повторенное столько же раз.

Выстроим одну из комбинаций из элементов в строчку. Домножив на , получим квадрат $k\times k$ элементов. То есть $kC_{n}^{k}$ — это множество квадратов. Теперь построим квадратную таблицу $n\times n$ (см.рис)

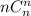В первой строке будут первые строчки большинства квадратов, кроме $C_{n}^{0}$ . Во второй строчке уже не будет $C_{n}^{1}$ , поскольку квадраты $1\times C_{n}^{1}$ целиком умещаются в первой строчке. И т.д. Причем будет отсутствовать вычитаемое $nC_{n}^{n}$ , т.к. этот квадрат содержит все строчки.

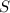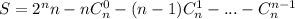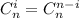Пусть искомая сумма . Сложив все строчки, получим $S=2^{n}n-nC_{n}^0-(n-1)C_{n}^1-...-C_{n}^{n-1}$ , поскольку $C_{n}^i=C_{n}^{n-i}$ , перепишем сумму:

$S=n2^n-S \Leftrightarrow S=2^{n-1}n$

0,0(0 оценок)

Ответ:

сюрприз23456789

31.01.2023 17:31

1. A) A - кол-во размещений из 8 по 3. Используя формулу находим:

8! / (8 - 3)! = 8! / 5! = 336

Б) C - кол-во сочитаний из 7 по 4. Используя формулу находим:

7! / ((7 - 4)! * 4!) = 35

В) P - кол-во перестановок. 6! = 720

2. а)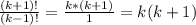 $\frac{(k + 1)!}{(k - 1)!} = \frac{k * (k + 1)}{1} = k(k + 1)$

б) (p - 5) - самое большое из представленных чисел, в произведениии есть все множители от 1 до (p - 5) включительно, а значит полученное произведение есть (p - 5)!

3. На первой позиции могут стоять все числа, кроме 0

На последующих позициях могут встречаться все числа кроме тех, что мы уже использовали, то есть на один вариант меньше каждый раз

Получаем:

1 позиция - 4 варианта (исключили ноль)

2 позиция - 4 варианта (исключили число на первой позиции, а ноль добавили)

3 позиция - 3 варианта (исключили числа на 1 и 2 позициях)

Итого получаем: 4 * 4 * 3 = 48 различных чисел

0,0(0 оценок)

Популярные вопросы: Математика