Это тест из Matetech: дальше таблица с допусками на атракционы. Иван повёл двоих своих сыновей Петю и Колю в парк аттракционов. Рост папы равен 190 см, рост Пети — 125 см, а рост Коли — 108 см. Папа весит 82 кг, Петя весит 30 кг, а Коля весит 18 кг. На аттракционах установлены ограничения по росту и весу посетителей, которым разрешено на них кататься.
Переводимо в десяткові дроби, 12.5% = 12.5%/100% = 0.125 і 5%=0.05
Нехай х - коефіцієнт пропорційності, тоді перше число дорівнює 0.125x, а друге - 0.05x. Середнє арифметичне двох чисел дорівнює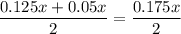
, що за умовою задачі становить 28, складаємо рівняння:
Значить маємо такі числа: 0.125 * 320 = 40 і 0.05*320 = 16.
Другий б.
Нехай перше число дорівнює x , тоді друге - у. Їх середнє арифметичне -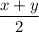
, що за умовою становить 28. Відомо, що 12,5% одного становить 5% другого, тобто 0.125x = 0.05y, складаємо систему рівнянь
Відповідь: 16.
В решении.
Пошаговое объяснение:
Задача 2.
х - решено задач в первый день.
2х - решено задач во второй день.
х+5 - решено задач в третий день.
По условию задачи уравнение:
х+2х+х+5=37
4х=32
х=8 - решено задач в первый день.
2*8=16 - решено задач во второй день.
8+5=13 - решено задач в третий день.
Проверка:
8+16+13=37 (задач), верно.
Задача 4.
х - яблок в 1 контейнере.
у - яблок во 2 контейнере.
Яблок в контейнерах поровну.
По условию задачи система уравнений:
х=у
х-13 = 3(у-31)
Раскрыть скобки:
х-13=3у-93
Подставить в уравнение значение х:
у-13=3у-93
у-3у= -93+13
-2у= -80
у= -80/-2
у=40 (кг) - было яблок во 2 контейнере первоначально.
Так как яблок в контейнерах было поровну, в 1 контейнере тоже было 40 кг яблок первоначально.
Проверка:
40-13=27
40-31=9
27:9=3 (раза) - во втором контейнере стало в 3 раза меньше яблок, чем в первом, верно.
Задание 5.
Решить уравнение:
(-2х-5)(0,3х+2,7)=0
-0,6х²-5,4-1,5х-13,5=0
-0,6х²-6,9х-13,5=0
Разделить уравнение (все части) на -0,6 для упрощения:
х²+11,5х+22,5=0, квадратное уравнение, ищем корни:
D=b²-4ac =132,25-90=42,25 √D= 6,5
х₁=(-b-√D)/2a
х₁=(-11,5-6,5)/2
х₁= -18/2
х₁= -9;
х₂=(-b+√D)/2a
х₂=(-11,5+6,5)/2
х₂= -5/2
х₂= -2,5.
Проверка путём подстановки вычисленных значений х в уравнение показала, что данные решения удовлетворяют данному уравнению.