СтогаллааChanel S. A. (произносится Шане́ль[3]) — французская компания по производству одежды и предметов роскоши, основанная модельером Коко Шанель в Париже в начале XX века. Бренд Chanel хорошо известен духами Chanel No. 5 и своими классическими костюмами. Шанель использовала цвета, традиционно ассоциирующиеся с мужественностью в Европе, такие как серый и темно-синий, чтобы обозначить смелый характер[7][8]. Примером является шерстяной костюм от Шанель — юбка до колен и жакет, отделанный и украшенный чёрной вышивкой и золотыми пуговицами. Дополнительными аксессуарами были двухцветные туфли-лодочки и украшения, обычно ожерелье из жемчуга и кожаная сумочка. Шанель отказалась одевать королевских особ, так как не желала заниматься дизайном бесплатно. Некролог WWD цитирует её так: «Эти принцессы и герцогини … они никогда не платят по счетам. Почему я должна отдавать им что-то даром? Никто никогда ничего мне не дарил.»Оборот: Около $1,089 млрд
Частное решение дифференциального уравнения:
Примечание:
Функция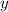 зависит от
зависит от  .
.
Прямое преобразование Лапласа (связь между оригиналами и изображениями):
По свойствам преобразования Лапласа:
Если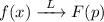 , то
, то 
Пошаговое объяснение:
Для нахождения частного решения данного дифференциального уравнения воспользуемся методом операционного исчисления, а именно преобразованием Лапласа:
Дифференцирования оригинала:
Раскладываем дробь на простейшие:
Таким образом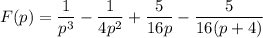
Выполним обратное преобразование Лапласа:
Тогда исходная функция равна: