Возьмём кукурузные палочки. Их состав: кукурузная крупа, сахар-песок,масло подсолнечное рафинированное дезодорированное,соль поваренная пищевая, вода питьевая, ароматизатор идентичный натуральному ванилин. У продукта очень большая калорийность- целых 460 кк, а это как 2 плитки шоколада! Данный продукт готов к употреблению, и его не нужно варить. Кушать его можно на завтрак, вместе с чаем или соком. Кукурузные палочки не стоит употреблять, так как в них содержится не натуральный ароматизатор, который очень вреден для организма. Он вредит организму тем, что откладывается на стенках желудка и застрявает там. А ещё у продукта очень большая калорийность.
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на , получаем
В левой части уравнения это ни что иное как формула производной частного, то есть :
Подсчитаем отдельный интеграл по частям.
2)
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена , перейдём к характеристическому уравнению: , корни которого и . Тогда общее решение диф. уравнения: и его первая производная .
Осталось найти константы C₁ и C₂ , подставляя начальные условия.
Их состав: кукурузная крупа, сахар-песок,масло подсолнечное рафинированное дезодорированное,соль поваренная пищевая, вода питьевая, ароматизатор идентичный натуральному ванилин.
У продукта очень большая калорийность- целых 460 кк, а это как 2 плитки шоколада!
Данный продукт готов к употреблению, и его не нужно варить. Кушать его можно на завтрак, вместе с чаем или соком.
Кукурузные палочки не стоит употреблять, так как в них содержится не натуральный ароматизатор, который очень вреден для организма. Он вредит организму тем, что откладывается на стенках желудка и застрявает там. А ещё у продукта очень большая калорийность.
1)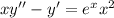
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на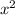 , получаем
, получаем
В левой части уравнения это ни что иное как формула производной частного, то есть :
Подсчитаем отдельный интеграл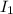 по частям.
по частям.
2)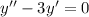
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена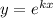 , перейдём к характеристическому уравнению:
, перейдём к характеристическому уравнению: 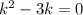 ,
, 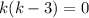 корни которого
корни которого 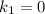 и
и 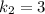 . Тогда общее решение диф. уравнения:
. Тогда общее решение диф. уравнения: 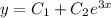 и его первая производная
и его первая производная 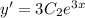 .
.
Осталось найти константы C₁ и C₂ , подставляя начальные условия.