Find the size of angle AED.
B
731
799
37
А
112
E
962
D

Пусть N имеет натуральные делители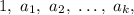 и их сумма равна A. Пусть, кроме того, 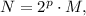где N - нечетное число.

Четные делители числа N имеют вид

Складывая четные делители группами в соответствие с тем, сколько множителей вида 2 в них есть, а потом складывая эти группы, получим

Требуется проверить, может ли

быть полным квадратом, то есть равняться B².

Конечно, такого быть не может, так как если перенести 1 направо, мы получили бы

Выражение, стоящее слева, делится на 2, но не делится на 4, выражение же, стоящее справа, или является нечетным (если B четное), или же делится не только на 4, а даже на 8 (хотя нам это и не нужно) -- ведь из двух последовательных четных чисел одно обязательно делится на 4.

Пошаговое объяснение:

1 Частные производные для F(x,y,z)=1

dFx=2x, dFy=-2y, dFz=-2z

Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(2,4,-4)

Уравнение плоскости A*x+B*y+C*z+D=0

A=Nx=2 B=Ny=4 C=Nz=-4

D=-(Nx*Mx+Ny*My+Mz*Mz)=-(2*1+4*(-2)+(-4)*2)=14

Плоскость 2x+4y-4z+14=0

Нормаль  (x-1)/2=(y+2)/4=(2-z)/4

2 Частные производные для F(x,y,z)=2

dFx=2xz-2y^3, dFy=-6xy^2, dFz=12z^3+x^2

Значения частных производных в заданной точке - это координаты вектора нормали для касательной плоскости N=(0,-6,13)

Уравнение плоскости A*x+B*y+C*z+D=0

A=Nx=0 B=Ny=-6 C=Nz=13

D=-(Nx*Mx+Ny*My+Mz*Mz)=-(0*1+(-6)*1+13*1)=-7

Плоскость -6y+13z-7=0

Нормаль  (1-y)/6=(z-1)/13

3. Производные на вложенном изображении.

Чтобы перейти к целым  числам значения производных в т (1,1,1) домножены на 6.

Вектор нормали тогда  N=(3,5,38)

Уравнение плоскости 3x+5y+38z-46=0

Нормаль (x-1)/3=(y-1)/5=(z-1)/38