функция у f x задана своим графиком укажите: а)область определения функции; б)при каких значениях х-2,50,f(x)<0; г)точки экстримума функции; д)наибольшее и наименьшее значение функции
Уравнение будет иметь ровно два корня, если значение -2а не будет входить в ОДЗ или будет равняться значению -4 или 2. То есть если будет входить в промежуток [-4 ; 2]
Подставим конечные значение промежутка :
-2a = -4
a = 2
----------
-2a = 2
a = -1 - наименьшее значение
_________________________________
Уравнение будет иметь три корня, если значение -2а входит в ОДЗ и не равняется значению -4 и 2. То есть если будет входить в промежуток (-∞ ; -4) U (2 ; +∞).
Самое наименьшее натурально значение а, которое входит в данный промежуток, это а = 3
1. Наименьшее значение а, при котором уравнение имеет два корня: a = -1
2. Наименьшее натуральное значение а, при котором уравнение имеет три корня: a = 3
4.3
ОДЗ : x ≥ 0
Для начала рассмотрим 2 случая, когда а = 4 и а = -4
1. При а = 4 : 0 = 8 , x ∈ ∅
2. При а = -4 : 0 = 0, x ∈ [0 ; +∞)
Теперь мы можем поделить обе части уравнения на (a^2-16) :
Уравнение будет иметь корни, если правая часть будет больше или равно 0 :
Уравнение будет иметь корни, если а ∈ (4 ; +∞) U {-4}
Наименьшее натуральное значение а, которое входит в данный промежуток, это а = 5
Пошаговое объяснение:
1)
перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
4(х+у)=5у
4х+4у=5у
4х=5у–4у
4х=у
х=у/4
Теперь подставим значение х в уравнение:
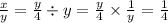
ОТВЕТ: х/у=1/42) Теперь это же значение у/4 подставим во второе уравнение:
(2√у+√х)/√х=(2√у+√у/√4)÷√у/√4=
=(2√у+√у/2)÷√у/2=((4√у+√у)/2)×2/√у=
=5√у/2×2/√у=5
ОТВЕТ: 5
ЗАДАНИЕ 2
во втором задании мы нашли чему будет =а: а=9b/4. Подставим его в первое уравнение:
1) a/b=9b/4÷b=9b/4×1/b=9/4=2,25
ОТВЕТ: 2,25
2) (а–b)/b=5/4 перемножим числитель и знаменатель соседних дробей между собой крест накрест и получим:
4(a–b)=5b
4a–4b=5b
4a=5b+4b
4a=9b
a=9b/4
теперь подставим значение а в уравнение:
(3√b+√a)/√a=(3√b+√9b/√4)/√9b/√4=
=(3√b+3√b/2)×√4/√9b
=((6√b+3√b)/2)×2/3√b=9√b/2×2/3√b=3
ОТВЕТ: 3
3.1
ОДЗ :
+ - +
-----------[-4]------------[2]---------------
x ∈ (-∞ ; -4] U [2 ; +∞)
Решим систему :
Уравнение будет иметь ровно два корня, если значение -2а не будет входить в ОДЗ или будет равняться значению -4 или 2. То есть если будет входить в промежуток [-4 ; 2]
Подставим конечные значение промежутка :
-2a = -4
a = 2
----------
-2a = 2
a = -1 - наименьшее значение
_________________________________
Уравнение будет иметь три корня, если значение -2а входит в ОДЗ и не равняется значению -4 и 2. То есть если будет входить в промежуток (-∞ ; -4) U (2 ; +∞).
Самое наименьшее натурально значение а, которое входит в данный промежуток, это а = 3
1. Наименьшее значение а, при котором уравнение имеет два корня: a = -1
2. Наименьшее натуральное значение а, при котором уравнение имеет три корня: a = 3
4.3
ОДЗ : x ≥ 0
Для начала рассмотрим 2 случая, когда а = 4 и а = -4
1. При а = 4 : 0 = 8 , x ∈ ∅
2. При а = -4 : 0 = 0, x ∈ [0 ; +∞)
Теперь мы можем поделить обе части уравнения на (a^2-16) :
Уравнение будет иметь корни, если правая часть будет больше или равно 0 :
Уравнение будет иметь корни, если а ∈ (4 ; +∞) U {-4}
Наименьшее натуральное значение а, которое входит в данный промежуток, это а = 5
ответ : при а = 5