9) Рассмотрим треугольник МОС, где С=60°, О=90°, М=30° соответственно. Катет ОС лежит напротив угла 30°, значит, он будет вдвое меньше гипотенузы: ОС=МС/2=4/2=2. Катет МО найдем по теореме Пифагора:
МО²=МС²-ОС²=4²-2²
МО=2√3.
Рассмотрим треугольник АСД, у которого два катета равны (т.к. в основании квадрат). Гипотезу в таком треугольнике нахрдят по формуле d=a√2.
d=AC=2OC=2×2=4.
Найдем катеты этого треугольника: а=d/√2=4/√2=2√2.
OK=AD/2=2√2/2 = √2
Найдем МК по теореме Пифагора:
МК²=МО²+ОК²=(2√3)²+(√2)²
МК=√14
ответ: МК=√14.
12) АВ=ВС=СА=12
R=a/2√3 = 12/2√3= 6/√3 = 2√3.
R=OD=2√3.
Найдем MD:
MD²=MO²+OD²=4²+(2√3)²
MD=2√7.
ответ: расстояние от точки М до прямой ВС равно 2√7
Пусть уравнение искомой кривой y=y(x). Рассмотрим произвольную точку на плоскости, производную в этой точке обозначим через Уравнение касательной к кривой будет иметь вид
Чтобы узнать, где эта касательная пересекается с осью OY, подставим x=0:
По условию
Поскольку - произвольная точка, можно последнее условие переписать в виде
Поскольку по условию кривая проходит через точку можем найти C:
И наконец, поскольку абсцисса точки которая лежит на кривой, положительна, и во всех других точках кривой абсцисса будет положительной, поэтому окончательный ответ такой:
9) Рассмотрим треугольник МОС, где С=60°, О=90°, М=30° соответственно. Катет ОС лежит напротив угла 30°, значит, он будет вдвое меньше гипотенузы: ОС=МС/2=4/2=2. Катет МО найдем по теореме Пифагора:
МО²=МС²-ОС²=4²-2²
МО=2√3.
Рассмотрим треугольник АСД, у которого два катета равны (т.к. в основании квадрат). Гипотезу в таком треугольнике нахрдят по формуле d=a√2.
d=AC=2OC=2×2=4.
Найдем катеты этого треугольника: а=d/√2=4/√2=2√2.
OK=AD/2=2√2/2 = √2
Найдем МК по теореме Пифагора:
МК²=МО²+ОК²=(2√3)²+(√2)²
МК=√14
ответ: МК=√14.
12) АВ=ВС=СА=12
R=a/2√3 = 12/2√3= 6/√3 = 2√3.
R=OD=2√3.
Найдем MD:
MD²=MO²+OD²=4²+(2√3)²
MD=2√7.
ответ: расстояние от точки М до прямой ВС равно 2√7
Пусть уравнение искомой кривой y=y(x). Рассмотрим произвольную точку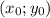
на плоскости, производную в этой точке обозначим через 
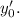Уравнение касательной к кривой будет иметь вид
Чтобы узнать, где эта касательная пересекается с осью OY, подставим x=0:
По условию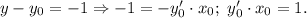
Поскольку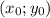
- произвольная точка, можно последнее условие переписать в виде
Поскольку по условию кривая проходит через точку
можем найти C:
И наконец, поскольку абсцисса точки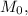
которая лежит на кривой, положительна, и во всех других точках кривой абсцисса будет положительной, поэтому окончательный ответ такой: