Вспомним единичную окружность, на которой определяются тригонометрические функции. Sin(x) измеряется по вертикальной оси.
Теперь осталось найти точки п/4 и 5п/4. Если угол в п радиан стягивает дугу в половину окружности, то п/4 будет стягивать четверть от половины. Очевидно, в наших координатах это будет такая точка на окружности, которая будет биссектрисой I четверти.
5п/4=п+п/4 - эта точка диаметрально противоположна точке п/4, потому что расположена как раз на п радиан дальше. Положительное направление обхода окружности у нас против часовой стрелки. Теперь мы можем отметить точки и оценить значение синуса в них.
Вспомним единичную окружность, на которой определяются тригонометрические функции. Sin(x) измеряется по вертикальной оси.
Теперь осталось найти точки п/4 и 5п/4. Если угол в п радиан стягивает дугу в половину окружности, то п/4 будет стягивать четверть от половины. Очевидно, в наших координатах это будет такая точка на окружности, которая будет биссектрисой I четверти.
5п/4=п+п/4 - эта точка диаметрально противоположна точке п/4, потому что расположена как раз на п радиан дальше. Положительное направление обхода окружности у нас против часовой стрелки. Теперь мы можем отметить точки и оценить значение синуса в них.
Вспомним единичную окружность, на которой определяются тригонометрические функции. Sin(x) измеряется по вертикальной оси.
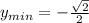 и
и 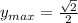
Теперь осталось найти точки п/4 и 5п/4. Если угол в п радиан стягивает дугу в половину окружности, то п/4 будет стягивать четверть от половины. Очевидно, в наших координатах это будет такая точка на окружности, которая будет биссектрисой I четверти.
5п/4=п+п/4 - эта точка диаметрально противоположна точке п/4, потому что расположена как раз на п радиан дальше. Положительное направление обхода окружности у нас против часовой стрелки. Теперь мы можем отметить точки и оценить значение синуса в них.
Вспомним единичную окружность, на которой определяются тригонометрические функции. Sin(x) измеряется по вертикальной оси.
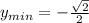 и
и 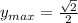
Теперь осталось найти точки п/4 и 5п/4. Если угол в п радиан стягивает дугу в половину окружности, то п/4 будет стягивать четверть от половины. Очевидно, в наших координатах это будет такая точка на окружности, которая будет биссектрисой I четверти.
5п/4=п+п/4 - эта точка диаметрально противоположна точке п/4, потому что расположена как раз на п радиан дальше. Положительное направление обхода окружности у нас против часовой стрелки. Теперь мы можем отметить точки и оценить значение синуса в них.