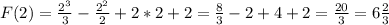Пошаговое объяснение:
Коли функция - первообразная для функции , то функция производной от функции .
Имея производную мы можем найти локальные максимумы и минимумы функции. Для этого найдем точки, в которых производная равняется 0.
- уравнение не имеет действительных корней.
Значит функция монотонно убывающая или монотонно возрастающая.
Ветви параболы направлены вверх, значит функция монотонно возрастающая.
Также это означает, что максимальное и минимальные значения функция принимает на концах заданного отрезка - [0; 2].
F(0) - минимальное значение на отрезке. Значит F(2) - максимальное значение на отрезке [0; 2].
Вычислим это значение.
Для начала, найдем функцию F(x). Для этого проинтегрируем её производную:
Это выражение задаёт целое семейство функций, различающихся на C = const.
Теперь найдем среди этого семейства нужную нам функцию. По условию у нас дано частное значение функции
Вычислим
Пошаговое объяснение:
Коли функция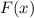 - первообразная для функции
- первообразная для функции 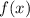 , то функция производной от функции
, то функция производной от функции 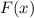 .
.
Имея производную мы можем найти локальные максимумы и минимумы функции. Для этого найдем точки, в которых производная равняется 0.
Значит функция монотонно убывающая или монотонно возрастающая.
Ветви параболы направлены вверх, значит функция монотонно возрастающая.
Также это означает, что максимальное и минимальные значения функция принимает на концах заданного отрезка - [0; 2].
F(0) - минимальное значение на отрезке. Значит F(2) - максимальное значение на отрезке [0; 2].
Вычислим это значение.
Для начала, найдем функцию F(x). Для этого проинтегрируем её производную:
Это выражение задаёт целое семейство функций, различающихся на C = const.
Теперь найдем среди этого семейства нужную нам функцию. По условию у нас дано частное значение функции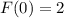
Вычислим