Находим координаты центра окружности, если прямые х=3 и у=1 являются касательными к окружности.
Рассмотрим рисунок (в приложении). На нём система координат Оху, прямые х=3 и у=1. На рисунке показано, что окружностей, которые могут касаться данных прямых на самом деле 4. Учитывая, что радиус окружности равен 5, находим координаты центров этих окружностей.
Касательные х=3 и у=1 пересекаются в точке (3;1). От этой точки вправо, влево, вверх и вниз отсчитываем по 5 единиц.
3+5=8
3-5=-2
1+5=6
1-5=-4
Получаем точки (8;6), (8;-4), (-2;6) и (-2;-4), которые и являются центрами окружностей.
(8;6), (8;-4), (-2;6) и (-2;-4)
Пошаговое объяснение:
(x-x₀)²+(y-y₀)²=25 - уравнение окружности
(x-x₀)²+(y-y₀)²= 5²
R=5 - радиус окружности
Находим координаты центра окружности, если прямые х=3 и у=1 являются касательными к окружности.
Рассмотрим рисунок (в приложении). На нём система координат Оху, прямые х=3 и у=1. На рисунке показано, что окружностей, которые могут касаться данных прямых на самом деле 4. Учитывая, что радиус окружности равен 5, находим координаты центров этих окружностей.
Касательные х=3 и у=1 пересекаются в точке (3;1). От этой точки вправо, влево, вверх и вниз отсчитываем по 5 единиц.
3+5=8
3-5=-2
1+5=6
1-5=-4
Получаем точки (8;6), (8;-4), (-2;6) и (-2;-4), которые и являются центрами окружностей.
Корень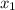 нам не подходит, так как параметры геометрических фигур не могут быть отрицательными.
нам не подходит, так как параметры геометрических фигур не могут быть отрицательными.
Значит, больший катет равен 35 см, а меньший:
35 см - 23 см = 12 см
Корень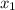 нам не подходит, так как параметры геометрических фигур не могут быть отрицательными.
нам не подходит, так как параметры геометрических фигур не могут быть отрицательными.
Значит, больший катет равен 15 см, а меньший:
15 см - 7 см = 8 см
Значит, одна часть это 2.
Первый катет =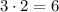 м.
м.
Второй катет =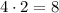 м.
м.
Хотя с этим заданием можно было справиться и проще. Треугольник со сторонами 6, 8, 10 является египетским. Это удвоенная версия треугольника 3, 4, 5.