а) По оси Х - t=2, S(2) = 8 км - через 2 часа - ОТВЕТ
б) Остановка - когда расстояние не изменяется. Находим и вычисляем время.
t2 = 7, t1 = 3
Время остановки - разность координат по оси Х - времени.
Т = 7 - 3 = 4 ч - остановка - ОТВЕТ.
в) Вопрос - 4 км от дома.
Находим на оси S значение S= 4 км. Проводим горизонтальную линию параллельно оси времени. Оказалось две точки пересечения с графиком пути. Проводим вертикальные линии и находим время.
ОТВЕТ: Через 1 час - уходил и через 10 часов - возвращался.
Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
РЕШЕНИЕ
Рисунок к задаче в приложении.
а) По оси Х - t=2, S(2) = 8 км - через 2 часа - ОТВЕТ
б) Остановка - когда расстояние не изменяется. Находим и вычисляем время.
t2 = 7, t1 = 3
Время остановки - разность координат по оси Х - времени.
Т = 7 - 3 = 4 ч - остановка - ОТВЕТ.
в) Вопрос - 4 км от дома.
Находим на оси S значение S= 4 км. Проводим горизонтальную линию параллельно оси времени. Оказалось две точки пересечения с графиком пути. Проводим вертикальные линии и находим время.
ОТВЕТ: Через 1 час - уходил и через 10 часов - возвращался.
Рисунок с решением задачи в приложении.
Пошаговое объяснение:
Мода (при ее наличии) всегда является вариантой ряда. Значит, мода - натуральное число, а тем более целое число.
Размах есть разность между наибольшей и наименьшей вариантой ряда. Значит, размах - разность двух натуральных чисел, то есть целое число.
Медиана ряда, состоящего из нечетного числа вариант, есть варианта, стоящая посередине ряда. Значит, медиана заданного ряда - натуральное число, следовательно и целое число.
Можно привести ряд, среднее арифметическое которого не будет целым числом.
Пример. Ряд 1, 1, ..., 1, 2.
Среднее арифметическое: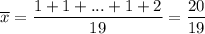
ответ: среднее арифметическое