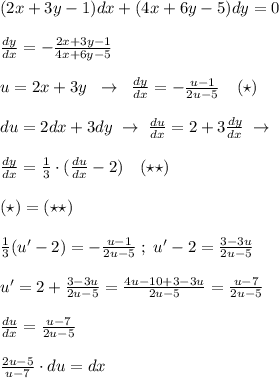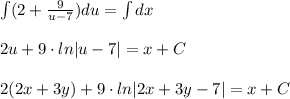Имеется такой дуффур: (2x+3y-1)dx+(4x+6y-5)dy=0. нужно решить его заменой переменных. понимаю, что нужно брать 2x-3y=u. но не могу никак понять момент, как дальше считать, как переходить от dx и dy к объяснить, без всяких лишних слов, именно момент перехода на данном примере.