Индийский д. р. капрекар известен своими работами по теории чисел. одна из его работ посвящена так называемому преобразованию капрекара. рассмотрим следующую операцию. пусть задано число xx. пусть mm — наибольшее число, которое можно получить из xx перестановкой его цифр, а mm — наименьшее число (это число может содержать ведущие нули). обозначим как k(x)k(x) разность m-mm−m, дополненную при необходимости ведущими нулями так, чтобы число цифр в ней было равно числу цифр в xx.
например, k(100) = 100 - 001 = 099k(100)=100−001=099, k(2414) = 4421 - 1244 = 3177k(2414)=4421−1244=3177.
капрекар доказал, что если начать с некоторого четырехзначного числа xx, в котором не все цифры равны между собой, и последовательно применять к нему эту операцию (вычислять k(x)k(x), k(k(x))k(k( …), то рано или поздно получится число 6174. для него верно равенство k(6174) = 7641 - 1467 = 6174k(6174)=7641−1467=6174, поэтому на нем процесс зациклится.
ваша состоит в том, чтобы написать программу, вычисляющую k(x)k(x) по числу xx.
введите целое число без ведущих нулей xx (1 \le x \le 10^91≤x≤10
9
).
в выходной файл выведите k(x)k(x).
Для начала поймём, что вообще представляют собой заданные уравнения системы
Таким образом, в системе оба неравенства задают пересечение указанного круга и указанной полоски.
Площадь круга радиуса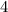 равна
равна 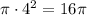 .
.
Отсюда, поскольку границы представляют собой прямые, то, при пересечении ими круга по диаметру получим нужное значение площади фигуры, т.е. половину от полной площади круга. Это можно достичь расположив центр круга в точках, где границы полоски пересекают ось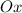 .
.
А именно при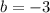 или
или 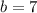 .
.
ответ.
(уравнение).
Пусть х км/ч - скорость товарного поезда, тогда 2х км/ч - скорость пассажирского поезда. Уравнение:
(х + 2х) · 2 = 270
2х + 4х = 270
6х = 270
х = 270 : 6
х = 45 (км/ч) - скорость товарного поезда
2х = 2 · 45 = 90 (км/ч) - скорость пассажирского поезда
(по действиям).
1) 270 : 2 = 135 км/ч - скорость сближения;
2) 1 : 2 - отношение скоростей;
3) 1 + 2 = 3 - всего частей;
4) 135 : 3 = 45 (км/ч) - скорость товарного поезда (1 часть);
5) 45 · 2 = 90 (км/ч) - скорость пассажирского поезда (2 части).
ответ: 45 км/ч и 90 км/ч.