Находим производную функции
y'=2x+2=2*(x+1)
Если , то производная
Так как производная положительна, функция возрастает
Находим наибольшее и наименьшее значения функции
Для этого найдем x, для которого y'=0
y'=0 при x=-1
Так как x=-1 принадлежит отрезку [-2; 0.4], то находим
y(-1)=(-1)^2+2*(-1)=-1
y(-2)=(-2)^2+2*(-2)=0
y(0.4)=(0.4)^2+2*0.4=0.96
Наибольшее значение функции на отрезке [-2; 0.4]
у(0.4)=0.96
Наименьшее значение функции на отрезке [-2; 0.4]
y(-1)=-1
Находим производную функции
y'=2x+2=2*(x+1)
Если , то производная
, то производная 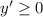
Так как производная положительна, функция возрастает
Находим наибольшее и наименьшее значения функции
Для этого найдем x, для которого y'=0
y'=0 при x=-1
Так как x=-1 принадлежит отрезку [-2; 0.4], то находим
y(-1)=(-1)^2+2*(-1)=-1
y(-2)=(-2)^2+2*(-2)=0
y(0.4)=(0.4)^2+2*0.4=0.96
Наибольшее значение функции на отрезке [-2; 0.4]
у(0.4)=0.96
Наименьшее значение функции на отрезке [-2; 0.4]
y(-1)=-1