3
Пошаговое объяснение:
Заметим, что данные прямые параллельны.
Запишем уравнение прямой, перпендикулярной исходным.
Поскольку k у данных прямых , то k перпендикулярной прямой будет , потому что в результате произведения мы должны получить -1.
Получим:
Здесь коэффициент b - любое число. Я возьму 0.
Продолжим решение.
Найдем пересечение перпендикулярной прямой с данными прямыми.
Для этого будем поочередно приравнивать уравнение перпендикулярной прямой с данными и решать систему.
Теперь без труда можно найти искомое расстояние:
Задача решена!
Среднее арифметическое трёх чисел равно 17.
Первое число больше третьего числа в 2,5 раз.
Второе число больше третьего в 0,5 раз(-а).
Найди первое, второе и третье число.
Решение.
Пусть третье число равно х.
Тогда первое число равно (х * 2,5).
Второе число равно (х * 0,5).
Зная, что среднее арифметическое трёх чисел равно 17, составим уравнение:
((х * 2,5) + (х * 0,5) + х ) : 3 = 17
(2,5х + 0,5х + х) : 3 = 17
4х : 3 = 17
4х = 17 * 3
4х = 51
х = 51 : 4
х = 12,75
Третье число равно 12,75
Первое число равно 12,75 * 2,5 = 31,875
Второе число равно 12,75 * 0,5 = 6,375
Проверка:
(31,875 + 6,375 + 12,75) : 3 = 51 : 3 = 17
Первое число равно 31,875
Второе число равно 6,375
3
Пошаговое объяснение:
Заметим, что данные прямые параллельны.
Запишем уравнение прямой, перпендикулярной исходным.
Поскольку k у данных прямых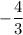 , то k перпендикулярной прямой будет
, то k перпендикулярной прямой будет  , потому что в результате произведения мы должны получить -1.
, потому что в результате произведения мы должны получить -1.
Получим:
Здесь коэффициент b - любое число. Я возьму 0.
Продолжим решение.
Найдем пересечение перпендикулярной прямой с данными прямыми.
Для этого будем поочередно приравнивать уравнение перпендикулярной прямой с данными и решать систему.
Теперь без труда можно найти искомое расстояние:
Задача решена!
Пошаговое объяснение:
Среднее арифметическое трёх чисел равно 17.
Первое число больше третьего числа в 2,5 раз.
Второе число больше третьего в 0,5 раз(-а).
Найди первое, второе и третье число.
Решение.
Пусть третье число равно х.
Тогда первое число равно (х * 2,5).
Второе число равно (х * 0,5).
Зная, что среднее арифметическое трёх чисел равно 17, составим уравнение:
((х * 2,5) + (х * 0,5) + х ) : 3 = 17
(2,5х + 0,5х + х) : 3 = 17
4х : 3 = 17
4х = 17 * 3
4х = 51
х = 51 : 4
х = 12,75
Третье число равно 12,75
Первое число равно 12,75 * 2,5 = 31,875
Второе число равно 12,75 * 0,5 = 6,375
Проверка:
(31,875 + 6,375 + 12,75) : 3 = 51 : 3 = 17
Первое число равно 31,875
Второе число равно 6,375
Третье число равно 12,75